Ранговая корреляция

Применение таблиц сопряженности для оценки взаимосвязи признаков

Таблицы сопряженности удобно применять для оценки взаимозависимости между двумя признаками 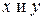, если число возможных значений каждого из них зафиксировано. Пусть проведено 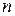наблюдений, для каждого из которых зафиксированы значения, принимаемые признаками 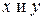. Обозначим через 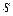число значений, принимаемых признаком 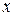, а через 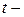число значений признака у. Имеющиеся результаты наблюдений оформим в виде таблицы.

Признак	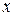Признак	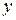Суммы по строкам
			.		.
			.		.
…	…	…	.	…	.	…	…
			.		.
…	…	…	.	…	.	…	…
			.		.
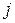
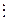
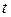
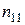
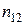
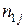
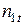
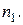
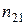
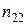
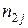
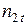
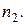
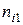
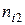
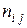
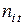
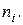
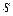
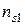
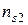
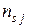
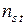
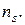
Сумма по столбцам			.		.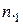

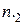
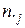
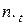
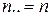
В первом столбце пронумерованы значения признака 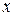от 1 до 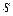; в первой строке – значения признака 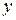от 1 до 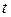. На пересечении 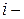й строки и 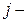го столбца стоит число 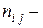это количество наблюдений, в каждом из которых признак 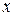принял 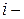e значение, а признак 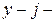е значение. Через 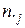обозначена сумма элементов столбца 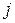, а через 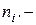сумма элементов строки .

Для оценки степени взаимозависимости между признаками вычисляется значение 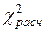по формуле

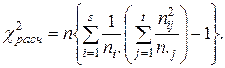(2.27)

Эта величина сравнивается со значением 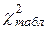, найденным из таблиц распределения 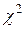по выбранному уровню значимости 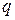и числу степеней свободы .

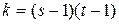Если 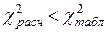, то можно констатировать отсутствие взаимовлияния между исследуемыми признаками.

Ту же методику можно использовать для непрерывных случайных величин, когда одна или обе исследуемые выборки имеют очень большие объемы. В этом случае диапазон изменения соответствующего признака делят на интервалы, которые и нумеруются в первом столбце и (или) первой строке таблицы.

Иногда требуется установить наличие взаимосвязи между двумя качественными признаками, т. е. признаками, которые не являются численно измеримыми. Например, качественными признаками являются фракционный состав технологической щепы, отражательная способность лакового покрытия, комфортность рабочего места и т. д. Исследуемые объекты в этом случае можно проранжировать, т. е. пронумеровать в порядке возрастания или убывания признака. Этот номер, присвоенный объекту, будем называть его рангом. Так как исследуются два признака, то каждому 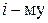объекту присваивается два ранга: 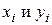в соответствии с признаками 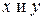. Таким образом, имеем две последовательности рангов:

по признаку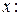
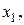
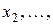
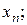
по признаку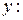

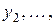
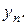
Одним из способов оценки связи между двумя качественными признаками является вычисление коэффициента ранговой корреляции Спирмена. Формула для него имеет вид

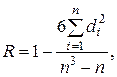(2.28)

где 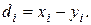(2.29)

Как и коэффициент корреляции, коэффициент 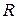изменяется в пределах от – 1 до +1, а его абсолютная величина пропорциональна степени зависимости между признаками .

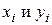Оценка значимости этого коэффициента проводится точно также, как и для обычного коэффициента корреляции 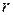. Эта проверка корректна в данном случае при 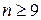. Если 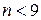, то можно воспользоваться специальными таблицами (см. Большев Л.Н., Смирнов Н.В. Таблицы математической статистики. М., 1983. 416 с.).

Коэффициент ранговой корреляции может использоваться и тогда, когда рассматриваемые признаки являются количественными, но для целей исследования достаточно проранжировать объекты по возрастанию или убыванию каждого из них.

2.14. Использование коэффициента конкордации для
обработки экспертных оценок при ранжировании

Рассмотрим задачу оценки степени согласованности мнений экспертов. Признаками в данном случае служат мнения экспертов. Эта задача часто встречается, например, в планировании эксперимента и прогнозировании. Пусть имеется 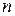факторов, влияющих на функционирование объекта .

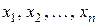Требуется выявить важнейшие из этих факторов, для того чтобы подвергнуть их дальнейшему исследованию. Каждому из 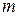экспертов предлагается список факторов с указанием диапазонов их варьирования. Эксперта просят приписать ранги этим факторам – пронумеровать их в порядке убывания степени их влияния на объект. Сведем результаты ранжирования, данные всеми экспертами, в таблицу.

Степень согласованности мнений экспертов характеризуется коэффициентом конкордации 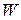, который вычисляется по формуле

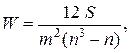(2.30)

где 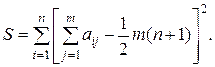(2.31)

Эксперты	Факторы
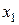
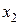
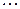
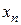
1-й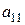
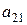
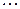
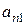
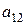
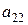
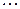
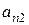
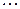
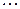
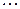
2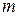-й
-й
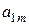
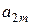
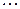
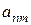
Суммы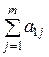

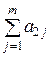
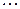
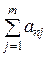
где 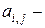ранг, присвоенный 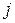-м экспертом -му фактору.

Величина 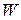может принимать значения в пределах 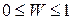. Чем ближе к 1 значение 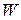, тем больше согласие между экспертами. Для оценки значимости коэффициента конкордации используется распределение 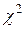(при 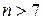). Вычисляется 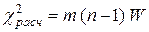, которое сравнивается с величиной 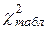, найденной при уровне значимости 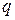и числе степеней свободы 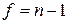. Если 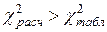то фиксируется согласие экспертов при данном уровне значимости.

Возможны случаи, когда эксперт признает влияние сразу нескольких факторов одинаковым и всем им присваивает один и тот же так называемый «связанный» ранг. Он равен среднему значению мест, поделенных этими факторами. Если, например три фактора делят 3, 4 и 5-е места, то каждому из них присваивается ранг, равный (3 + 4 + 5)/3 = 4. При наличии связанных рангов коэффициент конкордации вычисляется по формуле

(2.32)

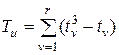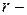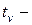где ; число типов связанных рангов в -строке; число повторений каждого из связанных рангов в -й строке; 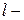число строк, содержащих связанные ранги. Остальные обозначения те же, что и в формуле (2.30).

Дата добавления: 2014-01-07