
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Транспортные задачи линейного программирования
|
|
|
|
В лесной и деревообрабатывающей промышленности, как и в других отраслях, часто приходится сталкиваться с задачами оптимизации перевозок разного рода грузов. Это может быть сухопутная транспортировка пиловочного сырья от леспромхозов к лесозаводам или сплав круглого леса от рейдов отправления к лесоперевалочным комбинатам, перевозки пиломатериалов от лесозаводов к потребителям, поставка мебельных изделий с фабрик в магазины и т. д. Во всех задачах подобного рода имеется несколько пунктов отправления (поставщиков), где сосредоточены запасы груза, и несколько пунктов назначения (потребителей груза). Необходимо составить экономичный план перевозок грузов от поставщиков к потребителям. В исследовании операций подобные задачи известны под названием транспортных задач (ТЗ).
Рассмотрим на числовом примере математическую модель транспортной задачи. Ее условия, а иногда и результаты решения будем записывать в транспортной таблице.
Пример. Предположим, что груз, подлежащий перевозке, сосредоточен в трех пунктах отправления: 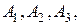 запасы груза в которых равны соответственно
запасы груза в которых равны соответственно 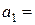 35,
35, 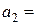 45 и
45 и 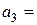 50 единиц (табл.).
50 единиц (табл.).
| Поставщик | Потребитель | ||||
| Обозначение | Запас груза | 
| 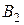
| 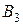
| 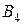
|
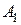
| 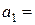 35 35
| ||||
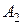
| 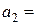 45 45
| ||||
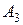
| 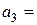 50 50
| ||||
| Потребность в грузе | 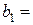 30 30
| 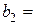 10 10
| 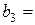 65 65
| 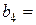 25 25
|
Груз надо доставить четырем потребителям: 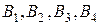 , подавшим заявки на 30, 10, 65 и 25 единиц груза соответственно. При этом суммарный запас груза у поставщиков равен сумме потребностей в нем у потребителей:
, подавшим заявки на 30, 10, 65 и 25 единиц груза соответственно. При этом суммарный запас груза у поставщиков равен сумме потребностей в нем у потребителей:
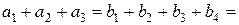 130.
130.
Известна стоимость перевозки единицы груза от каждого поставщика к каждому потребителю. Эти величины приведены в соответствующих клетках табл. Требуется указать, сколько груза должен получить каждый потребитель от каждого поставщика. При этом необходимо удовлетворить заявки всех потребителей, вывезти груз из всех пунктов отправления и обеспечить минимум затрат на перевозку всего груза. Предполагается, что для каждого маршрута эти затраты пропорциональны количеству перевозимого груза.
Обозначим через 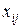 количество груза, перевозимое от
количество груза, перевозимое от 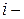 го потребителя к
го потребителя к 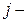 му поставщику. Эти искомые переменные служат элементами решения. В нашей задаче их будет 12:
му поставщику. Эти искомые переменные служат элементами решения. В нашей задаче их будет 12:
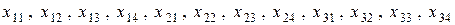 .
.
Запишем условие того, что выполнена заявка первого потребителя. Это означает, что количество груза, полученное им от первого, второго и третьего поставщиков, в сумме должно быть равно 30, т. е. 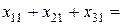 30.
30.
Аналогично записываются условия выполнения заявок для остальных потребителей: 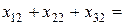 10;
10; 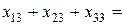 65;
65; 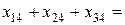 25.
25.
Рассмотрим ограничения, связанные с требованием вывезти весь груз каждого пункта отправления. Первый поставщик должен отправить в адрес первого, второго, третьего и четвертого потребителей соответственно 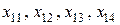 единиц груза, всего 35 единиц:
единиц груза, всего 35 единиц: 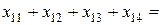 35. Соответствующие ограничения для остальных поставщиков имеют вид:
35. Соответствующие ограничения для остальных поставщиков имеют вид: 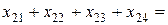 45;
45; 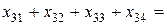 50.
50.
Для получения целевой функции задачи надо сложить затраты на перевозку по всем маршрутам: каждое слагаемое в этой сумме равно произведению количества перевозимого груза на стоимость перевозки единицы груза по данному маршруту. Так, стоимость перевозки груза из 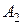 в
в 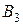 равна
равна 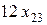 . Целевая функция поэтому имеет вид:
. Целевая функция поэтому имеет вид:

Полученные соотношения вместе с требованием неотрицательности переменных 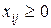 (
(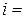 1, 2, 3;
1, 2, 3; 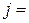 1, 2, 3, 4) образуют математическую модель транспортной задачи.
1, 2, 3, 4) образуют математическую модель транспортной задачи.
Рассмотрим теперь эту модель в общем виде. Имеем 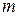 поставщиков и
поставщиков и 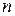 потребителей. Запасы груза у поставщиков равны соответственно
потребителей. Запасы груза у поставщиков равны соответственно 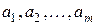 . Заявки потребителей составляют
. Заявки потребителей составляют 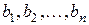 . Известна стоимость
. Известна стоимость 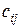 перевозки единицы груза от
перевозки единицы груза от 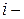 го поставщика к
го поставщика к 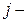 му потребителю,
му потребителю, 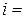 1, 2,...,
1, 2,..., 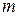 ;
; 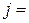 1, 2,...,
1, 2,..., 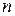 . Предполагается, что суммарные запасы груза равны суммарным потребностям в нем:
. Предполагается, что суммарные запасы груза равны суммарным потребностям в нем:
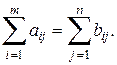 (5.24)
(5.24)
Искомый план перевозок, т. е. совокупность значений переменных 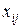 , должен удовлетворять тем же условиям, что и в рассмотренном выше числовом примере.
, должен удовлетворять тем же условиям, что и в рассмотренном выше числовом примере.
Запишем ограничения задачи, связанные с требованием удовлетворить заявку каждого потребителя:
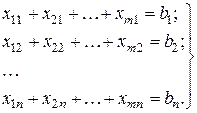 (5.25)
(5.25)
Требование вывезти весь груз из каждого пункта отправления реализуется следующим ограничениями:
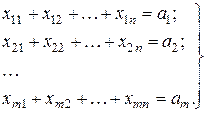 (5.26)
(5.26)
Целевая функция задачи
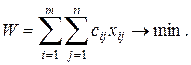 (5.27)
(5.27)
Переменные 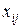 должны быть неотрицательными:
должны быть неотрицательными:
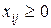 (
(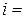 1, 2, …,
1, 2, …, 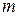 ;
; 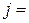 1, 2, …,
1, 2, …, 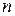 ). (5.28).
). (5.28).
Видно, что приведенная модель является задачей линейного программирования в силу линейности целевой функции и ограничений. Поэтому транспортные задачи в принципе можно решать любыми методами, пригодными для решения ЗЛП.
Рассмотренная выше модель транспортной задачи, предполагающая равенство суммарного спроса суммарным запасам, т. е. наличие ограничения (5.24), называется закрытой моделью транспортной задачи. Можно доказать, что эта задача всегда имеет оптимальное решение. Решение транспортной задачи часто называют планом перевозок.
Открытая модель транспортной задачи. Во многих задачах о перевозках не нужно требовать, чтобы весь запас груза у поставщиков был вывезен потребителям. Иными словами, имеется избыток груза. Поэтому условие (5.24) заменяется неравенством
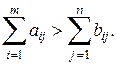 (5.29)
(5.29)
Вместо ограничений-равенств (5.26) также будут неравенства:
 (
(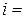 1, 2, …,
1, 2, …, 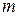 ). (5.30)
). (5.30)
Полученная модель, содержащая целевую функцию (5.27) и ограничения (5.25), (5.29), (5.30) и (5.28), называется открытой моделью транспортной задачи. Другой вариант открытой транспортной задачи (ТЗ) возникает, когда суммарный объем заявок превышает общий объем груза:
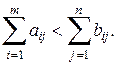 (5.31)
(5.31)
В этом случае ограничения (5.26) сохраняются, а заявки выполняются не полностью, поэтому равенства (5.25) заменяются неравенствами:
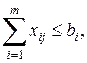 (
(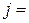 1, 2, …,
1, 2, …, 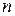 ). (5.32)
). (5.32)
Открытая транспортная задача легко сводится к рассмотренной ранее закрытой транспортной задаче. Для задачи с избытком груза вводится фиктивный (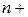 1)-й потребитель. Объем
1)-й потребитель. Объем 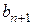 его заявки принимают равным разности между суммарным запасом груза поставщиков и суммарным объемом заявок потребителей:
его заявки принимают равным разности между суммарным запасом груза поставщиков и суммарным объемом заявок потребителей:
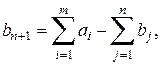
а стоимости перевозок от любого поставщика к этому фиктивному потребителю считают равными нулю:
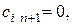 (
(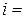 1, 2, …,
1, 2, …, 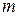 ).
).
Тем самым открытая транспортная задача преобразована в закрытую с тем же значением целевой функции.
Для открытой транспортной задачи с избытком заявок вводится
(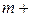 1)-й фиктивный поставщик с запасом груза равным
1)-й фиктивный поставщик с запасом груза равным
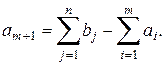
Стоимость перевозок от этого поставщика к любому потребителю принимают равной нулю.
Возможны и другие постановки этих задач. В задаче с избытком груза можно, например, учесть различные величины штрафов за единицу невывезенного груза от разных поставщиков. Задачу с избытком заявок можно рассмотреть с учетом сравнительной важности удовлетворения заявок разных потребителей. Эти постановки также сводятся к закрытой транспортной задаче.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 730; Нарушение авторских прав?; Мы поможем в написании вашей работы!