Непрерывные математические модели

Математические модели систем управления в пространстве состояний

МПС (Метод Пространств Состояний) применяется для исследования многомерных систем и ориентирован на использование компьютера.

В основу МПС положено понятие многомерного фазового пространства (или пространства состояний), по осям которого откладываются обобщённые фазовые координаты системы (или переменные состояния).

Состояние системы — совокупность минимального количества параметров, полностью определяющих поведение динамической системы.

Математическая модель системы при этом приводится к стандартному виду (или форме Коши):

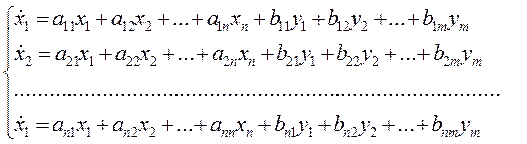(1)

Система уравнений (1) — это уравнение состояния в развёрнутой форме.

Соответствующая системе уравнений (1) структура системы:

В матричной форме систему уравнений (1) можно записать в следующем виде:

(2)

Здесь X, Y — вектора соответственно состояния и управления (смотри выше):

A — матрица системы; B — матрица управления.

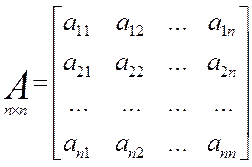
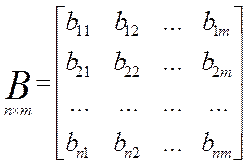
Уравнению состояния (2) соответствует следующая структура системы:

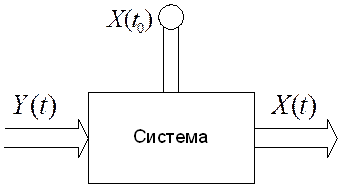
Система уравнений (1) и уравнение (2) соответствуют случаю, когда в качестве выходных переменных рассматриваются все переменные состояния.

В общем же случае количество выходных переменных зависит от рассматриваемой задачи и определяется линейной комбинацией переменных состояний 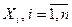и входных переменных (управляющих воздействий) .

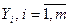Поэтому уравнение состояния системы в развёрнутой форме примет следующий вид:

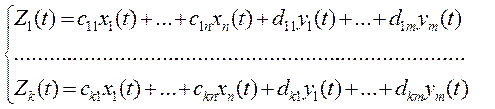(3)

Количество выходных переменных зависит от решаемой задачи.

Системе уравнений (3) будет соответствовать следующая структура системы:

В матричной форме уравнение состояния системы выглядит так:

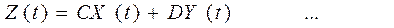(4)

Уравнению состояния (4) соответствует следующая структура системы:

Z(t) — вектор выхода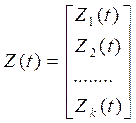

С — матрица системы; D — матрица управления.

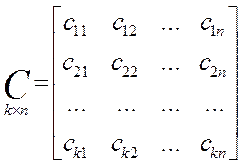
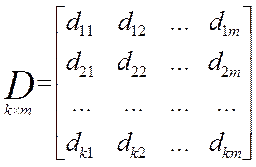
Пример 1.

Записать уравнения состояния в развёрнутой и матричной формах, составить схему (структуру) системы в переменных состояния непрерывной системы, математическая модель которой следующая:

.

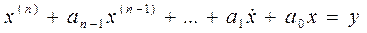Решение.

1. Вводим переменные состояния:

, , …, .

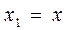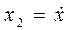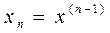2. Запишем уравнение состояния системы в развёрнутой форме Коши:

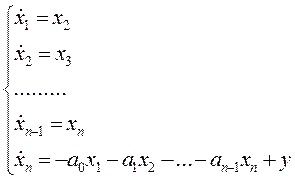
3. Запишем уравнение состояния в матричной форме:

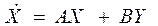
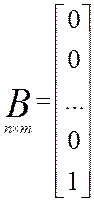
4. Составляем структуру системы в переменных состояния:

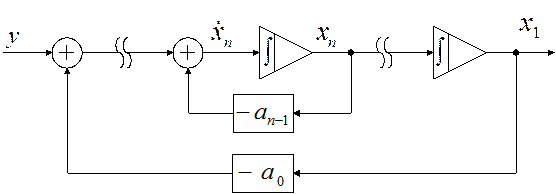
Пример 2.

Смотри условие примера 1, но .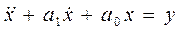

Решение.

1. Вводим переменные состояния:

, .

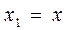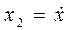2. Запишем уравнение состояния системы в развёрнутой форме Коши:

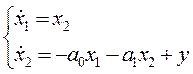
3. Запишем уравнение состояния в матричной форме:

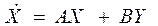
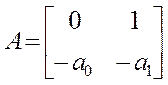
4. Составляем структуру системы в переменных состояния:

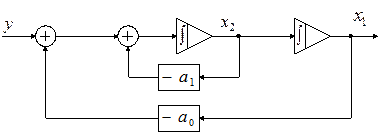
Пример 3.

По структуре системы в переменных состояния записать уравнения состояния в развёрнутой и матричной формах.

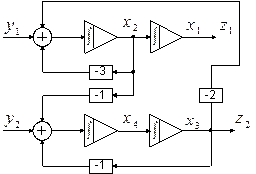
1.)

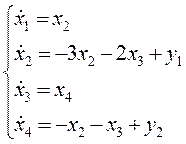
2.)

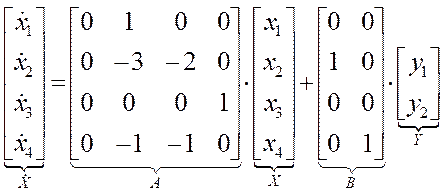
3.)

4.)

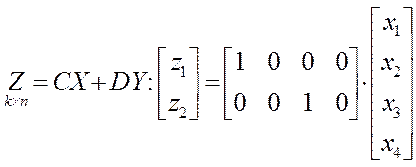
В замкнутой динамической системе выходной сигнал не может появиться на входе мгновенно для противодействия входному сигналу. Это обусловлено тем, что энергия в подсистемах не может изменяться мгновенно, то есть существует запаздывание. Энергия колеблется относительно некоторого уровня и при определённых условиях система из источника подавления колебаний становится их генератором, то есть оказывается неустойчивой.

Дата добавления: 2014-01-07