
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Принцип Даламбера
|
|
|
|
133. ПРИНЦИП ДАЛАМБЕРА ДЛЯ ТОЧКИ И МЕХАНИЧЕСКОЙ СИСТЕМЫ
Методы решения задач механики, которые до сих пор рассматривались, основываются на уравнениях, вытекающих или непосредственно из законов Ньютона, или же из общих теорем, являю следствием этих законов. Однако этот путь не является единственным. Уравнения движения или условия равновесия механической системы можно получить, положив в основу так называемые принципы механики. В этой главе будет рассмотрен один из общих принципов механики, называемый принципом Даламбера.
Найдем сначала выражение принципа для одной материальной точки. Пусть на материальную точку с массой m действует система активных сил, равнодействующую которых обозначим 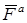 , и реакция связи
, и реакция связи 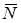 . Под действием этих сил точка будет двигаться по отношению к инерциальной системе отсчета с некоторым ускорением
. Под действием этих сил точка будет двигаться по отношению к инерциальной системе отсчета с некоторым ускорением  .
.
Введем в рассмотрение величину
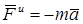 , (84)
, (84)
имеющую размерность силы. Векторную величину, равную по модулю произведению массы точки на ее ускорение и направленную противоположно этому ускорению, называют силой инерции точки.
Тогда оказывается, что движение точки обладает следующим свойством: если в любой момент времени к действующим на точку активным силам и реакции связи присоединить силу инерции, то полученная система сил будет уравновешенной, т. е.
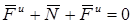 . (85)
. (85)
Это положение выражает принцип Даламбера для материальной точки. Нетрудно убедиться, что оно эквивалентно второму закону Ньютона и наоборот.
Рассмотрим теперь механическую систему, состоящую из n материальных точек. Выделим какую-нибудь из точек системы с массой mk. Под действием приложенных к ней внешних и внутренних сил 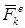 и
и  (в которые входят и активные силы, и реакции связей) точка будет двигаться по отношению к инерциальной системе отсчета с некоторым ускорением
(в которые входят и активные силы, и реакции связей) точка будет двигаться по отношению к инерциальной системе отсчета с некоторым ускорением  . Введя для этой точки силу инерции
. Введя для этой точки силу инерции  , получим согласно равенству (85), что
, получим согласно равенству (85), что
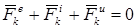 . (85)
. (85)
т. е. что 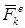 ,
,  и
и 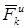 образуют уравновешенную систему сил. Повторяя такие рассуждения для каждой из точек системы, придем к следующему результату, выражающему принцип Даламбера для системы: если в любой момент времени к каждой из точек системы кроме действующих на нее внешних и внутренних сил присоединить соответствующие силы инерции, то полученная система сил будет уравновешенной и к ней можно применять все уравнения статики.
образуют уравновешенную систему сил. Повторяя такие рассуждения для каждой из точек системы, придем к следующему результату, выражающему принцип Даламбера для системы: если в любой момент времени к каждой из точек системы кроме действующих на нее внешних и внутренних сил присоединить соответствующие силы инерции, то полученная система сил будет уравновешенной и к ней можно применять все уравнения статики.
Из статики известно, что геометрическая сумма сил, находящихся в равновесии, и сумма их моментов относительно любого центра О равны нулю. Тогда на основании принципа Даламбера должно быть:
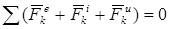
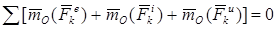 (86)
(86)
Введем обозначения:
 (87)
(87)
Величины  ,
, 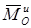 представляют собою главный вектор и, момент относительно центра О системы сил инерции. В результате учитывая, что геометрическая сумма внутренних сил и моментов равны нулю, получим из равенств (86):
представляют собою главный вектор и, момент относительно центра О системы сил инерции. В результате учитывая, что геометрическая сумма внутренних сил и моментов равны нулю, получим из равенств (86):
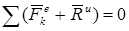 ,
,  (88)
(88)
Уравнениями (88) особенно удобно пользоваться при изучении движения твердого тела или системы твердых тел. Для полного изучения движения любой изменяемой системы этих уравнений будет недостаточно, так же как недостаточно уравнений статики для изучения равновесия любой механической системы.
134. ГЛАВНЫЙ ВЕКТОР И ГЛАВНЫЙ МОМЕНТ СИЛ ИНЕРЦИИ
Сравнивая первое из равенств (88) с уравнением 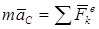 выражающим теорему о движении центра, найдем, что
выражающим теорему о движении центра, найдем, что
 (89)
(89)
т. е. главный вектор сил инерции механической системы (в частности, твердого тела) равен произведению массы системы (тела) на ускорение центра масс и направлен противоположно этому ускорению. Если ускорение 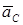 разложить на касательное и нормальное, то вектор
разложить на касательное и нормальное, то вектор  разложится на составляющие
разложится на составляющие
 . (89')
. (89')
Сравнив теперь второе из равенств (88) с уравнением  выражающим теорему моментов, и учтя, что аналогичным будет соотношение для моментов относительно оси, получим:
выражающим теорему моментов, и учтя, что аналогичным будет соотношение для моментов относительно оси, получим:
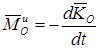 и
и  (90)
(90)
т.е. главный момент, сил инерции механической системы (твердого тела) относительно некоторого центра О или оси z равен взятой со знаком минус производной по времени от кинетического момента системы (тела) относительно того же центра или той же оси.
Приведение сил инерции твердого тела. Систему сил инерции твердого тела можно заменить одной силой, равной  и приложенной в произвольно выбранном центре О, и парой с моментом, равным
и приложенной в произвольно выбранном центре О, и парой с моментом, равным 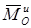 . Рассмотрим несколько частных случаев.
. Рассмотрим несколько частных случаев.
1. Поступательное движение. В этом случае ускорения всех точек тела одинаковы и равны ускорению 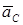 центра масс С тела. Тогда все силы инерции
центра масс С тела. Тогда все силы инерции  образуют систему параллельных сил, аналогичных силам тяжести
образуют систему параллельных сил, аналогичных силам тяжести  , и поэтому, как и силы тяжести, имеют равнодействующую, проходящую через точку С.
, и поэтому, как и силы тяжести, имеют равнодействующую, проходящую через точку С.
Следовательно, при поступательном движении силы инерции твердого тела приводятся к равнодействующей, равной  и проходящей через центр масс тела.
и проходящей через центр масс тела.
2. Вращательное движение. Пусть твердое тело имеет плоскость материальной симметрии Оху и вращается вокруг оси Оz, перпендикулярной этой плоскости (рис. 343, где показано сечение тела плоскостью Оху). Если привести силы инерции к центру О, то вследствие симметрии результирующая сила и пара будут лежать в плоскости Оху и момент пары будет равен 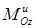 . Тогда, так как
. Тогда, так как 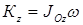 , то по второй из формул (90)
, то по второй из формул (90)
 , (91)
, (91)
где 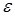 — угловое ускорение тела.
— угловое ускорение тела.
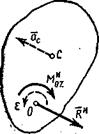 Следовательно, система сил инерции такого вращающегося приводится к силе
Следовательно, система сил инерции такого вращающегося приводится к силе  , определяемой формулой (89) и приложенной в точке О (рис. 343), и к паре с моментом
, определяемой формулой (89) и приложенной в точке О (рис. 343), и к паре с моментом 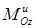 , определяемым формулой (91), лежащей в плоскости симметрии тела.
, определяемым формулой (91), лежащей в плоскости симметрии тела.
3. Вращение вокруг оси, проходящей через центр масс тел. Если тело, вращается вокруг оси Оz, проходящей через центр масс С тела, то  = 0, так как
= 0, так как 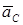 =0. Следовательно, в этом случае система сил инерции тела привод к одной только паре с моментом
=0. Следовательно, в этом случае система сил инерции тела привод к одной только паре с моментом 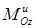 , лежащей в плоскости симметрии тела.
, лежащей в плоскости симметрии тела.
4. Плоскопараллельное движение. Если тело имеет плоскость симметрии и движется параллельно этой плоскости то, очевидно, система сил инерции тела приведется к лежащим в плоскости симметрии силе, равной  и приложенной в центре масс С тела, и паре с моментом
и приложенной в центре масс С тела, и паре с моментом 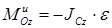 .
.
135. РЕШЕНИЕ ЗАДАЧ
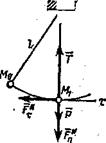 Задача 155. Решить задачу 107 с помощью принципа Даламбера Решение. Изображаем груз в том положении, для которого надо найти натяжение нити (рис. 344). На груз действуют сила тяжести
Задача 155. Решить задачу 107 с помощью принципа Даламбера Решение. Изображаем груз в том положении, для которого надо найти натяжение нити (рис. 344). На груз действуют сила тяжести 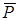 и реакция нити
и реакция нити  . Присоединяем к этим силам нормальную и касательную силы инерции
. Присоединяем к этим силам нормальную и касательную силы инерции  и
и  . Полученная система сил, согласно принципу Даламбера, будет находиться в равновесии. Приравнивая нулю сумму проекций всех этих сил на нормаль М1О получим
. Полученная система сил, согласно принципу Даламбера, будет находиться в равновесии. Приравнивая нулю сумму проекций всех этих сил на нормаль М1О получим
 .
.
Так как 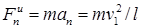 , где v1 — скорость груза в положения M1, то
, где v1 — скорость груза в положения M1, то
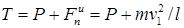
Таким образом, мы получили для T то же выражение, что и в задаче 107. Определяя теперь, как и в задаче 107, величину v1 с помощью теоремы об изменении кинетической энергии, найдем искомый результат.
Уравнение в проекции на касательную дает 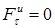 . Этот результат получается потому, что в точке M1 производная dv/dt = 0, так как в этой точке модуль скорости имеет максимальное значение.
. Этот результат получается потому, что в точке M1 производная dv/dt = 0, так как в этой точке модуль скорости имеет максимальное значение.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 684; Нарушение авторских прав?; Мы поможем в написании вашей работы!