Первое начало термодинамики

В основе т.д. лежат 2 основных. закона, или начала термодинамики и тепловая теорема Нернста или теорема начала термодинамики.

Эти законы являются обобщением большого количества ва экспериментального материала, накопленного человечеством.

1-й з-н т.д. –это з-н сохранения и превращения энергии при разнообразных процессах, протекающих в природе, энергия не возникает из нечего и не уничтожается, но превращается лишь из одного вида в другие.Для того, чтобы записать это в математическую ф-лу рассмотрим как происходит изменение вн. энергии системы.

Внутренняя энергия газа будет повышается при его нагревании т.е. когда газу сообщается какое-то кол-во теплоты.Т.о. подвод к системе или отвод от нее теплоты являетсяся одним из способов изменения вн.энергии.Вторым способом изменения вн.энергии системы яв-ся совершение системой некоторой работы, или же совершение работы над системы.

Действительно, если совершить работу быстро сжав газ, он нагреется, т.е. его вн. энергия возрастет. Наоборот, если предоставить газу расширеться, не подводя к нему теплоты, газ будет охлаждаться т.е. его вн. энергия будет убывать.

Передача теплоты и совершение работы – это две формы движения материи в результате которого и только благодаря которым изменяется вн.энергия системы.

Учитывая процессы теплообмена и совершения работы и соответствующие знаки можно записать з-н сохранения эн-ии в виде

ΔU=ΔQ-ΔA (1)

Изменения вн.эн=ии ΔU равно разности сообщаемого телу кол-ва теплоты ΔQ и произведённой телом мех-ой работы ΔA. Этот закон можно переписать в виде

ΔQ=ΔU+ΔA (2)

Кол-во теплоты, собщаемое телу (ΔQ), идёт на увеличение его вн. эн-ии (ΔU) и на совершение телом работы (ΔA).

Выр-ие (2) удобно записать для малого изменения состояния системы, вызванного сообщением ей малого кол-ва тепла δQ и совершения системой тел работы δА

ΔQ=dU+ δА

Различие в знаках ΔQ, dU и δА имеет глубокий физич-ий смысл. Дело в том, что вн. эн-ия системы явл-ся однозначной функцией состояния. Сл-но, при совершении системой любого процесса, в результате которого она возвращается в исходное сост-е, полное изменние её вн.эн-ии равно 0

Газу расширятся, не подводя к нему теплоты, газ будет охлаждаться, т. е. его внутренняя энергия будет убывать.

Передача теплоты и совершение работы – это две формы движения материи, в результате которых и благодаря которым изменяется внутренняя энергия системы.

Учитывая процессы теплообмена и совершения работы и соответствующие знаки можно записать закон сохранения энергии в виде

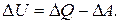(1)

Изменение внутренней энергии равно разности сообщенного телу количества теплоты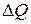и произведенной телом механической работы. Этот закон можно переписать в виде

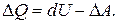(2)

Количество теплоты сообщенное телу (, идет на увеличение его внутренней энергии (и на совершение телом работы .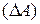

Выражение (2) удобно записать для малого изменения составляющих системы, вызванного сообщением ей малого количества тепла 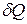и совершения системой, ей работы

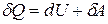
Различие в знаках и dU имеет глубокий физический смысл. Дело в том, что внутренняя энергия системы является однозначной функцией состояния. Следовательно, при совершении системой любого процесса, в результате которого она возвращается в исходное состояние, полное изменение ее внутренней энергии равно нулю

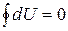
что является необходимым и достаточным условием для того чтобы выражение dU представляло полный дифференциал. Оказывается ни теплота, ни работа этим свойством не обладают и 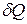и не являются полными дифференциалами. Отсюда получаем что ни работа ни количество переданного тепла не тождественно с энергией. Они имеют тот смысл, что их сумма определяет изменение энергии.

Исторически установления закона сохранения энергии (I начало) было связано с неудачами осуществления такой машины, которая совершала бы работу, не затрачивая при этом никакого вида энергии и не получая извне тепла. В термодинамике такая машина названа вечным двигателем – перпетуум mjbile 1^ого рода.

Как мы уже отмечали, при возвращении системы в исходное состояние ее энергия принимает прежнее значение. Поэтому для периодически действующих машин к концу каждого периода 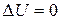, и совершенная ею работа может быть получена лишь за счет переданного извне количества тепла Δ Q,либо за счет каких-либо других дополнительных внешних источников энергии.

Т. к. передача тепла есть тоже передача энергии, то можно вообще говорить о переданной энергии и формулировать закон сохранения энергии (I начало термодинамики) в следующей форме.

Невозможно построить перпетуум мобиле (perpetuum mobile) 1-ого рода, т. е. телсой периодически действующей машины, которая производила бы работу в большем количестве, чем количество поглощенной им извне энергии.

Работа газа при изменении его объема.

Графическое изображение термодинамических процессов и работы

Рассмотрим газ, заключенный в цилиндр с подвижным невесомым поршнем имеющим площадь S. Пусть на газ действует только внешнее давление. Начальные параметры состояния газа p₁, V₁, T₁. Вначале поршень находится в равновесии с внешней средой (р₁=р). Если к газу подвести тепло 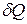, он нагреется и давление его повысится. Равновесие поршня нарушится и он переместится на расстояние dx, так, чтобы давление газа вновь стало равным р. расширяясь газ совершает работу против сил внешнего давления

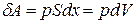
Оказывается приведенная формула справедлива не только для газов, но и вообще для любого термодинамического тела, совершающего произвольный процесс.

Для изучения и сравнения различных термодинамических процессов их удобно изображать графически. Зная уравнение состояния данного тела и решив его относительно Т, можно любой паре значений p и V сопоставить определенные значения третьего параметра состояния – температуры. Поэтому для графического описания процесса достаточно указать, как изменяется при этом два параметра, например, давление и удельный объем.

В двумерной системе координат, осями которой служат давление и удельный объем, зависимость р от V в процессе изображается некоторой кривой.

Точки C₁(p₁ V₁) и C₂(p₂ V₂) характеризуют начало и конец состояния тела, а кривые С₁, С ₂ изображают рассмотренный термодинамический процесс.

Важно отметить, что графически можно изображать только равновесные процессы, при которых изменение состояния тела протекает очень медленно, строго говоря, бесконечно медленно. Все реальные процессы протекают с конечной скоростью и поэтому неравновесные.

В случае неравновесных процессов не имеет смысла говорить о давлении, удельном объеме и температуре всего тела, т.к. они будут различны в разных его частях. Поэтому неравновесные процессы нельзя изображать графически. Однако в ряде случаев, неравновесностью реальных процессов можно пренебречь. Так, например, в рассмотренном выше примере сжатия газа это можно сделать, если скорость движения поршня во много раз меньше скорости звука в газе, размеры цилиндра не велики.

Диаграмма (p-V) позволяет дать графическую интерпретацию элементарной работы . Произведение p^.dV измеряется площадь заштрихованной криволинейной трапеции, а работа расширения от состояния С ₁ до состояния С ₂ площадью S’ V ₁ C ₁ C ₂ V ₂ равно определенному интеграллу

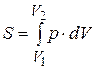
Отсюда ясно, что работа зависит не только от начального состояния тела, но и от того, каков термодинамический процесс, т. е. какой кривой происходит изменение состояния.

Из уравнения площадей под кривыми C ₁ L ₁ C ₂, C ₁ L ₂ C ₂ и C ₁ L ₃ C ₂ следует

Если процесс происходит по замкнутой кривой 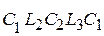и газ вернулся в первоначальное состояние, то полная работа, совершенная газом не равна нулю. В результате сложения положительной работы расширения dV>0, изображенное площадью и отрицательной работой сжатия, изображенной площадью 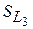получится полная работа процесса, изображенная заштрихованной площадью.

Работа совершаемая газом в изопроцессах

(Изопроцессы идеального газа)

Большую роль в изучении тепловых свойств вещества играет понятие теплоемкости. Удельной теплоемкостью называется физическая величина, численно равная количеству теплоты, которое надо сообщить единице массы этого вещества для увеличения ее температуры на один градус (^оК)

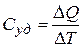
Для газов удобно пользоваться молярной теплоемкостью, характеризующейся количеством теплоты нужным для нагревания одного кмоля данного вещества на один градус.

Теплоемкость газа существенно зависит от того, как меняется состояние газа в процессе нагревания. Рассмотрим для простоты идеальный одноатомный газ. Если мы будем нагревать его при V =const, то все подводимое тепло будет идти только на увеличение внутренней энергии газа. 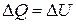При этом температура газа будет возрастать соответственно с увеличением его внутренней энергии. Давление газа также будет возрастать. Теплоемкость газа при V =const обозначают через С _V.

Если в процессе нагревания p =const, газ расширяется и выполняет работу против сил внешнего давления. Т. к. внутренняя энергия не зависит от его объема, то количество теплоты, необходимое для ее увеличения, останется тем же. Следовательно, при p =const для нагревания газа до той же температуры затрачивается больше количества теплоты. Поэтому теплоемкость при p =const C_P будет больше, чем C _V (C _P> C _V)

Величина C _P и C _V для идеального газа связаны простым соотношением. Для вывода этого соотношения рассмотрим кмоль идеального газа, называемого при V= const. Поскольку при этом .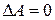

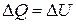и

Рассмотрим теперь 1 кмоль газа в цилиндре с поршнем, т. е. при p= const

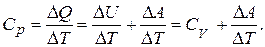
Для идеального газа p,V и Т связаны между собой уравнением Клапейрона – Менделеева, которое для 1 моля газа имеет вид.

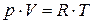
После нагревания при р= const до температуры Т+∆Т газ займет объем

pV RT

=

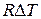
Отсюда искомая величина

Т. о. —формула Майера

Из последнего выражения можно дать простую формулировку смысла универсальной газовой постоянной.

Универсальная газовая постоянная R численно равна работе расширения кмоля идеального газа при его нагревании на один градус при постоянном давлении.

Среди многочисленных применений термодинамики (расчет тепловых двигателей, холодильных машин и т. д.) наиболее часто приходится иметь дело с изопроцессами в газах. Так называют процессы в газах когда один из параметров (p,V и T) сохраняется постоянным.

Изохорический процесс

Этот процесс осуществляется при нагревании газа в замкнутом объеме. Поскольку .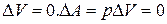

Уравнение первого начала термодинамики имеет вид

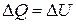
Т. е. все сообщенное тепло газу идет на увеличение его внутренней энергии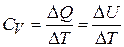

Изобарический процесс ( p= const)

Работа изображается площадью прямоугольника

I^ое начало термодинамики применительно к процессу

Подводимое к газу тепло частью расходуется на увеличение внутренней энергии (нагревание), а частью на совершение работы.

Как уже было доказано для идеального газа .

Дата добавления: 2014-01-07