Движение заряда в постоянном однородном магнитном поле

Рассмотрим заряд е движущийся в однородном постоянном магнитном поле. Применяя второй закон Ньютона к движению заряда, получим уравнение, описывающее движение заряда в магнитном поле:

(19.1)

Представим скорость движения заряда векторной суммой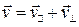

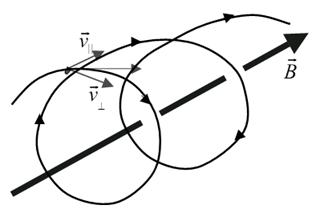В направлении, параллельном магнитному полю 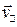, проекция силы, действующей со стороны поля на движущийся заряд, равна нулю, что вытекает из свойств векторного произведения:.

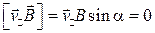Тогда:

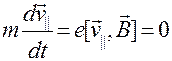(19.2)

Поэтому составляющая скорости, параллельная вектору индукции магнитного поля, не меняется .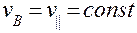

Для составляющей скорости, перпендикулярной к направлению магнитного поля 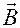, имеем уравнение:

(19.3)

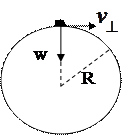
Ускорение равно и направлено перпендикулярно скорости частицы. В этом случае частица движется в магнитном поле с постоянной по модулю скоростью , траектория движения в плоскости перпендикулярной к полю – окружность. Тогда ускорение , и

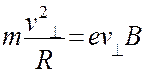
откуда радиус описываемой окружности равен:

(19.4)

Учитывая (19.4), получаем частоту вращения заряда вокруг силовой линии индукции магнитного поля – так называемую, циклотронную частоту вращения:

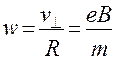(19.5)

2 Взаимодействие токов. Закон Ампера

Рассмотрим взаимодействие постоянных токов.

Так как каждый носитель тока в проводнике испытывает действие силы со стороны магнитного поля, то в результате магнитное поле действует на сам проводник с током.

Поместим проводник с током в магнитное поле. На каждый заряд действует сила Лоренца:

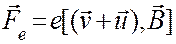(19.6)

где 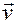- скорость хаотического движения, 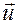- скорость дрейфа носителей. Если S – сечение проводника, n – концентрация носителей, то на элемент тока длиной dl будет действовать сила:

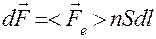(19.7)

dV=Sdl – элементарный объём проводника. Средняя сила действующая на заряд:

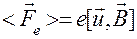(19.8)

т.к 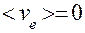‑ скорость хаотического движения.

Тогда, сила действующая на элемент тока равна:

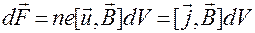(19.9)

Можно записать силу, действующую на тонкий проводник с током в магнитном поле. Для этого объёмный элемент тока выразим через линейный элемент тока:

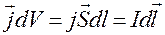(19.10)

Тогда сила, действующая на проводник длиной 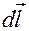, определяется:

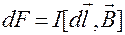(19.11)

Сила, действующая на проводник конечной длины:

(19.12)

В общем случае необходимо учитывать векторный характер подынтегрального выражения при получении результирующей силы.

Если имеем участок прямого проводника с током длины l, находящийся в постоянном магнитном поле, тогда величина силы, действующей на этот участок, получается из интегрирования (19.12) и скалярно равна:

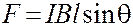(19.13)

где угол θ – угол между направлением силовых линий индукции магнитного поля и прямым участком проводника.

Эти соотношения (19.9) ‑ (19.13) и определяют закон взаимодействия токов – закон Ампера (1820г.).

Дата добавления: 2014-01-07