Выполнимость. общезначимость

Интерпретация формулы логики предикатов в виде суждения.

Формула есть перевод содержательного рассуждения в формальное рассуждение. Формула имеет смысл только тогда, когда имеется какая-нибудь интерпретация входящих в нее символов. Каждая интерпретация состоит в указании множества М изменения предметных переменных и задании отношения между переменными с помощью предикатов.

Для данной интерпретации формула представляет собой высказывание, если переменные связаны кванторами, а если есть свободные переменные, то формула есть предикат, который может быть истинным для одних значений переменных из области интерпретации и ложным для других.

Пример 2.22.

Пусть М – множество целых положительных чисел, и дан предикат A (x, y) = “ x 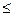y ”.

Рассмотрим следующие формулы:

1) A (x, y);

2) " yA (x, y);

3) $ x " yA (x, y).

Первая формула – это предикат, который является истинным высказыванием для всех пар целых положительных чисел (a, b), таких, что a 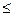b.

Вторая формула – предикат “Для всякого целого положительного числа y имеет место x 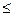y ”, который является истинным только для x = 1.

Третья формула – высказывание “Существует такое x, что для всякого y имеет место x 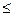y ”. Оно является истинным и соответствует тому, что на множестве М есть наименьшее число (единица).

Пусть задаио множество M изменения предметных переменных формулы A (x ₁, x ₂,..., x_n), т. е. (x ₁, x ₂,..., x_n) M.

Определение 2.7. Формула A называется выполнимой в данной интерпретации, если существует набор значений переменных (a ₁, a ₂,..., a_n) M, для которого A (a ₁, a ₂,..., a_n) = И.

Определение 2.8. Формула A называется истинной в данной интерпретации, если A (x ₁, x ₂,..., x_n) = И на любом наборе своих переменных (x ₁, x ₂,..., x_n) M.

Определение 2.9. Формула A называется общезначимой или тождественно-истинной, если она истинна в каждой интерпретации.

Определение 210. Формула A называется выполнимой, если существует интерпретация, для которой она выполнима.

Проблема разрешимости для логики предикатов, так же, как и для логики высказываний (см. раздел 1.5) заключается в том, чтобы установить, является ли произвольная формула тождественно-истинной.

Но, если для логики высказываний эта проблема решается положительно, то для логики предикатов неразрешимость этой проблемы устанавливает следующая теорема:

Теорема 2.4. (Теорема Черча). Не существует алгоритма, который для любой формулы логики предикатов устанавливает, общезначима она или нет.

Однако, для одноместных предикатов проблема разрешимости решается положительно.

В общем случае выделение общезначимых формул логики предикатов возможно в рамках аксиоматического подхода, который будет рассмотрен ниже (см. раздел 3.3).

Контрольные вопросы к теме 2

1. Какие из следующих утверждений верны:

а) Предикат есть сложное высказывание, состоящее из простых высказываний.

б) Предикат есть высказывание, зависящее от параметров.

в) Высказывание есть 0-местный предикат.

г) Высказывание есть одноместный предикат.

2. Выберите правильный вариант ответа 1 – 4 для следующих вопросов:

а) Обобщением какой операции является связывание квантором общности?

б) Обобщением какой операции является связывание квантором существования?

Варианты ответа: 1 – дизъюнкция; 2 – конъюнкция; 3 – импликация; 4 – эквивалентность.

3. Какие из следующих формул логики предикатов являются равносильными:

а) ¬" xA (x) и $ x (¬ A (x)); б) ¬$ xA (x)) и $ x ¬ A (x)); в)" x (A (x)V B) и " xA (x)V B;

г) $ x (A (x)& B (x)) и $ xA (x)&$ xB (x); д)" x " yA (x, y) и " y " xA (x, y);

е) $ x $ yA (x, y) и $ y $ xA (x, y);

ж) $ x " yA (x, y) и " y $ xA (x, y).

4. Какие из следующих формул логики предикатов являются приведенными и какие – нормальными:

а) ¬" xA (x) V $ x " yA (x, y); б) $ y $ xA (x, y)& " y $ zB (y, z); в) $ x " y $ z (A (x, y) & B (y, z)).

Дата добавления: 2014-01-07