Основные формулы теории надежности

Основные количественные показатели надежности.

ЛЕКЦИЯ 5 (Акимов стр.19….24)

Если ана­лизируются закономерности отказов, ликвидируемых в эксплуа­тации путем перерегулировок, замены отдельных агрегатов, устранения негерметичностей и т. п., то в данном случае двигатель является изделием восстанавливаемым. Но и при отказах такого рода, если изучать закономерности работы до первого отказа,можно считать двигатель невосстанавливаемым изделием. Когда рассматриваются закономерности надежности при наличии восстановления, это оговаривается специально.

В задачах надежности время работы до отказа считается не­прерывной случайной величиной. Если при 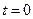изделие начало работать, а при наработке 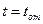потеряло работоспособность, то наступление отказа есть событие, заключающееся в том, что 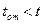т. е. в том, что случайная величина 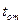оказалась не больше времени t.

Одним из основных количественных показателей надежности является вероятность того, что время безотказной работы окажет­ся больше заданного времени t:

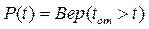. (2.1)

Функция 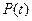называется вероятностью безотказной работы (часто — функцией надежности, иногда — просто надежностью). Вероятностью отказа называется, соответственно, функция

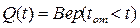. (2.2)

Так как при любом значении наработки t изделие может быть только или работоспособным, или потерявшим работоспособность, то вероятность того, что оно находится в одном из двух указанных состояний, есть вероятность достоверного события и, следователь­но,

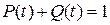. (2.3)

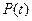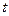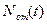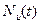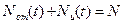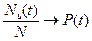Вероятность безотказной работы может быть приближен­но определена из рассмотрения результатов эксплуатации или испытаний достаточно большого числа N однотипных устройств. Если в любой момент времени функция определяет число отказавших к этому моменту устройств, a - число исправ­ных и , то при 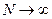, т. е.

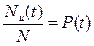. (2.4)

Очевидно, что 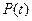— убывающая функция времени, так как при отсутствии восстановления число исправных изделий уменьшается. При отсутствии наработки (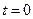) отказов еще не может быть и .

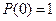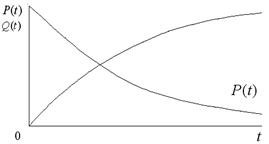
Рис. 2.1. Примерный вид функци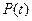й и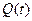

Примерный вид функци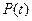й и 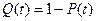показан на рис. 2.1. Кривую 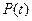иногда называют кривой убыли, подчеркивая этим тот факт, что она отражает убывание со временем числа изделий, сохранивших работоспособность.

2.Плотность вероятности отказов или плотность распределения времени безотказной работы 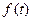является одной из важных характеристик надежности. В теории вероятностей плотностью распределения называется функция, равная пределу отношения вероятности того, что случайная величина находится в каком-то малом интервале, к продолжительности этого интервала. Если случайная величина - время работы до отказа, то плотность распределения времени безотказной работы

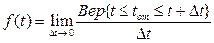, (2.5)

т. e. 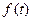есть предел отношения вероятности того, чтовремя рабо­ты до отказа будет находиться в малом интервале 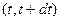, к величине этого интервала. При 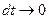можно записать, что

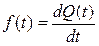. (2.6)

Приближенно определить значения функции 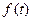можно опытным путем для отдельных интервалов наработки :

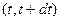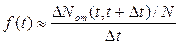(2.7)

где 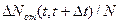есть опытная величина вероятности отказа за время 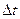, a 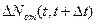- число отказов в интервале .

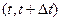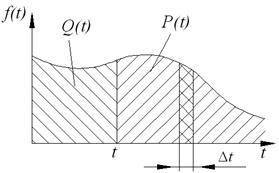
Рис.2.2 Кривая плотности вероятности отказов

Чем больше N и меньше 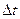, тем точнее формула (2.7).(плотно заштрихованная на рис. 2.2 площадка). Соответственно вероятность отказа за время t есть интеграл от 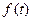, взятый для интервала от 0 до t:

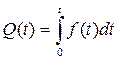. (2.8)

При 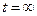, то вероятность отказа равна единице. Из этого следует, что вся площадь под кривой 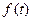всегда равна единице. Но

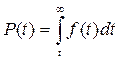. (2.9)

Выражение (2.9) означает, что вероятность безотказной работы за время t равна всей площади под кривой 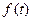правее абсциссы t (см. рис. 2.2).

Так как из теории вероятностей известно, что плотность распределения есть производная функции распределения 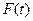, то из сопоставления этого факта с выражениями (2.6) и (2.8) очевидно, что в задачах надежности интегральная функция распределения имеет смысл вероятности отказа, т. е. 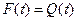и .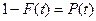

3. Введем теперь понятие о важнейшей и очень распространенной характеристике надежности — интенсивности отказов. Смысл этой характеристики в оценке вероятности отказа в интервале 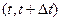изделий, безотказно проработавших до начала этого интервала, т. е. не вышедших из строя за время t. для изделий проработавших время

Функция интенсивности отказов 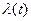может быть определена как

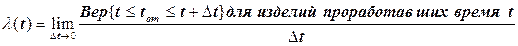. (2. 10)

Иными словами 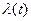есть предел отношения условной вероятности отказа в интервале 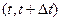[при условии безотказной ра­боты в интервале 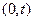] к длине этого интервала.

По данным эксплуатации или испытаний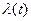для отдельных интервалов наработки можно приближенно определить, используя следующее выражение:

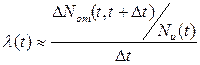. (2.11)

В формуле (2.11) 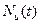и 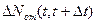имеют тот же смысл, что и в (2.4) и (2.7) соответственно, a 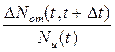— вероятность отказа в интервале 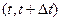изделий, благополучно доработавших до начала этого интервала.

Интенсивность отказов характеризует надежность в каждый данный момент времени. Поэтому ее иногда называют опасностью отказа. 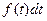есть вероятность отказа за время 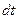, как бы­ло показано выше. Но это — вероятность отказа любого из общего числа рассматриваемых устройств (априорная вероятность). Ин­тенсивность же отказов характеризует условную (апостериорную) вероятность отказа в малом интервале времени, так как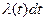есть, как видно из выражения (2.11), вероятность отказа за 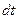только тех устройств, которые остались работоспособными к моменту наработки t.

Найдем связь между 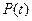, 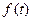и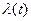. Для этого воспользуем­ся упомянутой выше схемой испытаний N устройств, 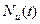из ко­торых в каждый момент времени исправны, a 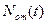- отказали. Так как 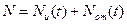, то

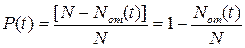, (2. 12)

где аналогично выражению (2.4) .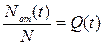

Дифференцируя левую и правую части уравнения (2.12), можно записать

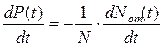. (2. 13)

Так как правая часть выражения (2.13) по абсолютной величине есть предел выражения (2.7), то можно записать

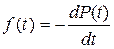. (2. 14)

Из полученного выше можно записать, что

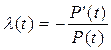. (2.16)

Формула (2.16) дает наиболее общее выражение для интенсивности отказов. Другое общее соотношение, связывающее плотность, интенсивность и вероятность безотказной работы, следует из выражений (2.14) и (2.16):

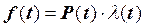. (2.17)

Теперь, разделяя переменные в уравнении (2.16), проинтегри­руем его в пределах от 0 до t и соответственно от 1 до :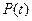

,

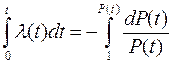Получаем 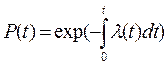. (2.18)

Формула (2.18) выражает надежность через интенсивность отказов в общей форме. Это выражение является одним из наиболее практически важных соотношений в теории надежности.

Все обсужденные выше характеристики надежности являются функциональными зависимостями, практическое определение которых обработкой статистических данных достаточно трудоемко, а в некоторых случаях весьма затруднительно. Поэтому наряду с такими характеристиками, как 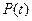, , 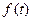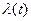широкое исполь­зование в практике находит критерий надежности, выраженный числовой величиной, — среднее время безотказной работы или наработка на отказ Т.

Среднее время безотказной работы является по смыслу средним значением наработки до отказа, т. е. средним значением случайной величины или математическим ожиданием. Из теории вероятности известно, что математическое ожидание для непрерывной случайной величины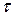 выражается следующим интегралом:

.

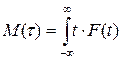Так как случайная величина 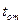существует только в интерва­ле (0, 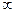), то

.

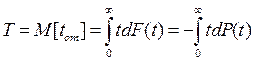Интегрируя по частям, получаем

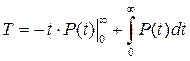. (2.19)

При конечных значениях 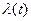функция 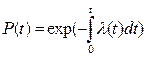при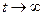стремится к 0 быстрее, чем 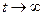. Поэтому первый член в формуле (2.19) равен 0 и она перепишется как

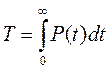. (2.20)

Наиболее точный способ определения Т опытным путем:

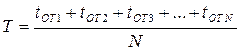(2.21)

Формулы (2.17), (2.18), (2.20) являются наиболее общими соотношениями теории надежности.

Дата добавления: 2014-01-07