Гипотезы. Различия между распределениями недостоверны (судя по точке максимального накопленного расхождения между ними)

Различия между распределениями недостоверны (судя по точке максимального накопленного расхождения между ними).

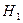: Различия между распределениями достоверны (судя по точке максимального накопленного расхождения между ними).

Для применения критерия Колмогорова—Смирнова необходи­мо соблюдать следующие условия:

1. Измерение может быть проведено шкале интервалов и отношений.

2. Выборки должны быть случайными и независимыми.

3. Желательно, чтобы суммарный объем двух выборок ≥ 50. С увеличением объема выборки точность критерия повышается.

4. Эмпирические данные должны допускать возможность упорядочения по возрастанию или убыванию какого-либо призна­ка и обязательно отражать какое-то его однонаправленное изменение. В том случае, если трудно соблюсти принцип упорядоченности признака, лучше использовать критерий хи -квадрат.

Этот критерий используется для решения тех же задач, что и критерий xи -квадрат. Иначе говоря, с его помощью можно срав­нивать эмпирическое распределение с теоретическим или два эмпирических распределения друг с другом. Однако если при применении хи -квадрат мы сопоставляем частоты двух распреде­лений, то в данном критерии сравниваются накопленные (куму­лятивные) частоты по каждому разряду (альтернативе). При этом если разность накопленных частот в двух распределениях оказы­вается большой, то различия между двумя распределениями яв­ляются существенными.

Задача 8.12. Предположим, что в эксперименте психологу не­обходимо использовать шестигранный игральный кубик с цифрами на гранях от 1 до 6. Для чисто­ты эксперимента необходимо получить «идеаль­ный» кубик, т.е. такой, чтобы при достаточно большом числе подбрасываний, каждая его грань выпадала бы примерно равное число раз. Задача состоит в выяснении того, будет ли данный ку­бик близок к идеальному?

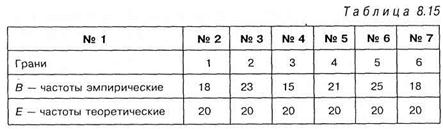
Решение. Подбросим кубик 120 раз и сравним полученное эмпирическое распределение с теоретическим. Поскольку теоретическое распределение являет­ся равновероятным, то соответствующие теоре­тические частоты равны 20. Распределение эмпи­рических и теоретических частот представим со­вместно в таблице 8.15:

Для подсчета по критерию Колмогорова—Смирнова необхо­димо провести ряд преобразований с данными таблицы 8.15. Представим эти преобразования в таблице 8.16 и объясним их получение:

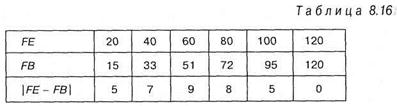
Символом FE в таблице 8.16 будем обозначать накопленные теоретические частоты. В таблице они получаются следующим об­разом: к первой теоретической частоте 20, добавляется вторая частота, также равная 20, получается число 20 + 20 = 40. Число 40 ставится на место второй частоты. Затем к числу 40 прибавляется следующая теоретическая частота, полученная величина 60 — ставится на место третьей теоретической частоты и так далее.

Символом FB в таблице 8.16 обозначаются накопленные эм­пирические частоты. Для их подсчета необходимо расположить эмпирические частоты по возрастанию: 15, 18, 18, 21, 23, 25 и затем по порядку сложить. Так, вначале стоит первая частота равная 15, к ней прибавляется вторая по величине частота и по­лученная сумма 15 + 18 = 33 ставится на место второй частоты, затем к 33 добавляется 18 (33 + 18 = 51), полученное число 51 ставится на место третьей частоты и т.д.

Символом |FE - FB| в таблице 8.16 обозначаются абсолютные величины разности между теоретической и эмпирической часто­той по каждому столбцу отдельно.

Эмпирическую величину этого критерия, которая обознача­ется как D _эмп получают используя формулу (8.13):

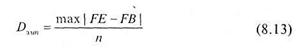
Для её получения среди чисел |FE - FB| находят максималь­ное число (в нашем случае оно равно 9) и делят его на объем выборки п. В нашем случае п = 120, поэтому

Для этого критерия таблица с критическими значениями дана в Приложении 1 под № 13. Из таблицы 13 Приложения 1 следует, однако, что в том случае, если число элементов выбор­ке больше 100, то величины критических значений вычисляются по формуле (8.14):

Иными словами, вместо привычных табличных значений вы­числяются величины D_кр подстановкой величины объема выбор­ки вместо символа п.

В нашем случае п = 120, поэтому D_кр для 0,05 равно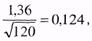

и D_кp для 0,01 равно 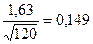, или в привычной форме записи:

В нашем случае D_эмп оказалось равным 0,075, что гораздо меньше 0,124, иначе говоря, эмпирическое значение критерия Колмогорова-Смирнова попало в зону незначимости. Таким об­разом, гипотеза Н ₁ отклоняется и принимается гипотеза 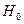о том, что теоретическое и эмпирическое распределения не отли­чаются между собой. Следовательно, можно с уверенностью ут­верждать, что наш игральный кубик «безупречен».

Дата добавления: 2014-01-07