Случай несвязных выборок

В общем случае формула для расчета по t -критерию Стьюден­та такова:

где

Рассмотрим сначала равночисленные выборки. В этом случае п 1 = п 2 =п, тогда выражение (9.2) будет вычисляться следую­щим образом:

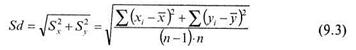
В случае не равночисленных выборок п 1 ≠ п 2, выражение (9.2) будет вычисляться следующим образом:

В обоих случаях подсчет числа степеней свободы осуществля­ется по формуле:

где п 1 и п 2 соответственно величины первой и второй выборки.

Понятно, что при численном равенстве выборок k= 2 · п - 2.

Рассмотрим пример использования t -критерия Стьюдента для несвязных и неравных по численности выборок.

Задача 9.1. Психолог измерял время сложной сенсомоторной реакции выбора (в мс) в контрольной и эк­спериментальной группах. В экспериментальную группу (X) входили 9 спортсменов высокой ква­лификации. Контрольной группой (Y) являлись 8 человек, активно не занимающиеся спортом. Психолог проверяет гипотезу о том, что средняя скорость сложной сенсомоторной реакции выбо­ра у спортсменов выше, чем эта же величина у людей, не занимающихся спортом.

Решение. Результаты эксперимента представим в виде таб­лицы 9.1, в которой произведем ряд необходи­мых расчетов:

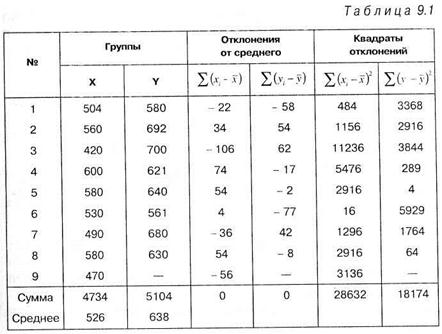
Средние арифметические составляют в экспериментальной

группе, в контрольной группе .

Разница по абсолютной величине между средними

.

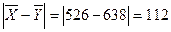Подсчет выражения 9.4 дает:

Тогда значение t_эмп, вычисляемое по формуле (9.1), таково:

Число степеней свободы k = 9 + 8-2= 15. По таблице 16 Приложения 1 для данного числа степеней свободы находим:

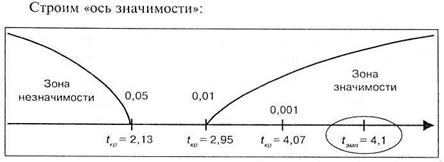
Таким образом, обнаруженные психологом различия между экспериментальной и контрольной группами значимы более чем на 0,1% уровне, или, иначе говоря, средняя скорость сложной сенсомоторной реакции выбора в группе спортсменов суще­ственно выше, чем в группе людей, активно не занимающихся спортом.

В терминах статистических гипотез это утверждение звучит так: гипотеза Н₀ о сходстве отклоняется и на 0,1% уровне значи­мости принимается альтернативная гипотеза Н ₁ - о различии между экспериментальной и контрольными группами.

Дата добавления: 2014-01-07