Динамическая модель машинного агрегата

Краткое содержание: Динамическая модель машинного агрегата и ее параметры. Методика приведения масс. Методика приведения сил. Прямая задача динамики машин. Уравнения движения машинного агрегата в энергетической и дифференциальной форме. Пример на определение параметров динамической модели.

Динамическая модель машинного агрегата и ее параметры

В общей постановке динамика – изучение каких-либо процессов или явлений в функции времени. Динамическая модель – модель системы, предназначенная для исследования ее свойств в функции времени (или модель системы, предназначенная для исследования в ней динамических явлений).

Механизм машинного агрегата обычно является многозвенной системой, нагруженной силами и моментами, приложенными к различным ее звеньям. Рассмотрим в качестве примера силовую установку, где ДВС через редуктор приводит в движение рабочую машину. Определение закона движения такой сложной многозвенной системы представляет собой сложную задачу, однако данный машинный агрегат имеет одну степень свободы. Это значит, что, прежде всего, необходимо определить закон движения всего лишь одного звена, которое будет являться начальным. Такая постановка задачи приводит к мысли, заменить весь сложный многозвенный механизм одним условным звеном. Если заданный механизм имеет звено, совершающее непрерывное вращательное движение, то именно его и целесообразно выбирать в качестве начального.

При замене механизма динамической моделью необходимо выполнить следующие условия:

1. Закон движения входного звена механизма должен совпадать с законом движения модели его заменяющей.

Т.е. кинематические характеристики модели и звена приведения механизма должны быть одинаковымиили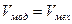

Положение модели в пространстве и положение звена приведения должны быть одинаковыми или .

2. Модель должна быть нагружена условной силой или моментом, называемым приведенным моментом или силой и определяемым из условия равенства мгновенных мощностей модели и машинного агрегата. Т.е. 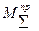или являются эквивалентом всей заданной нагрузки приложенной к машинному агрегату.

3. Модель должна обладать условной массой или моментом инерции, называемым приведенной массой или приведенным моментом инерции и определяемым из условия равенства кинетических энергий модели и машинного агрегата. Т.е. или 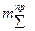являются эквивалентом все инерционности машинного агрегата.

Т.о. замена механизма динамической моделью заключается в:

1. Замене всех реальных сил силовым фактором.

2. Замене масс всех звеньев приведенным инерциальным фактором.

Замена сил и масс называется приведением, звено которое выбрано в качестве начального – звеном приведения.

Если звено приведения совершает вращательное движение, то все силы приводятся к приведенному моменту, а массы – к приведенному моменту инерции, если звено приведения совершает поступательное движение или приведение осуществляется к точке, то все силы приводятся к приведенной силе, а массы – к приведенной массе.

Методика приведения сил

Методика приведения сил основана на равенстве элементарных работ или мгновенных мощностей исходного машинного агрегата и заменяющей его динамической модели.

Вид нагрузки	Элементарная работа	Мгновенная мощность
сила
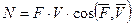
знак определяется знаком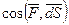
-
применяется в том случае, когда сила или перемещение (скорость) имеют проекцию только на одну координатную ось, например сила веса, знак определяется знаками соответствующих проекций
Момент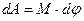
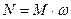
знак определяется направлением поворота (угловой скорости), если момент сонаправлен с изменением угла поворота (угловой скорости), то работа (мощность) положительна, если нет – отрицательна

Окончательно

• для механической системы

Элементарная работа	Мгновенная мощность

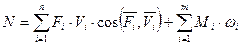
• для модели

Элементарная работа	Мгновенная мощность

Приравнивая элементарные работы или мгновенные мощности исходного машинного агрегата и динамической модели, получаем формулу для определения приведенного суммарного момента динамической модели

Элементарная работа	Мгновенная мощность

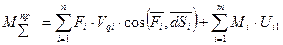
В любом машинном агрегате приведенный суммарный момент динамической модели состоит из 2-х частей:

,

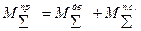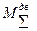- суммарный момент движущих сил является постоянной величиной для рабочих машин (насосов, станков, компрессоров и пр.) и приложен к звену приведения; переменная величина для двигателей и приводится к начальному звену.

- суммарный момент сил полезного сопротивления является постоянной величиной для двигателей и приложен к звену приведения; переменная величина для рабочих машин (насосов, станков, компрессоров и пр.) и приводится к начальному звену.

Методика приведения масс

Методика приведения масс основана на равенстве кинетических энергий исходного машинного агрегата и заменяющей его динамической модели. Запишем для них уравнение изменения кинетической энергии.

Кинетическая энергия:

Движение твердого тела	Кинетическая энергия
Вращение
Поступательное движение
Плоское движение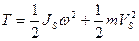

Окончательно

• для механической системы

,

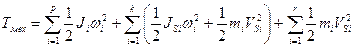где 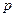- число звеньев двигающихся вращательно, - момент инерции этих звеньев относительно точки закрепления, если центр масс не лежит на оси, то применяют теорему Штейнера –Гюйгенса:

,

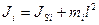где - расстояние от центра масс звена до оси вращения, - момент инерции звеньев относительно центра масс, - число звеньев, движущихся плоско, - число звеньев движущихся поступательно.

• для модели (вращающейся)

Модель будет энергетически эквивалентна рассматриваемой механической системе, если правые и левые части уравнений изменения кинетической энергии для модели и для системы будут соответственно равны.

Подставляя в равенства, записанные ранее выражения для кинетических энергий, получим:

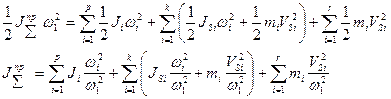
Из уравнения для левых частей получаем формулу для определения приведенного суммарного момента инерции динамической модели

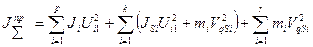
В любом машинном агрегате приведенный суммарный момент инерции динамической модели состоит из 2-х частей:

- приведенный момент инерции первой группы звеньев. К первой группе звеньев относятся те звенья, которые имеют постоянное передаточное отношение со звеном приведения.

- приведенный момент инерции второй группы звеньев. Ко второй группе звеньев относятся те звенья, которые не имеют постоянного передаточного отношения со звеном приведения.

Прямая задача динамики машин.

Прямая задача динамики машины, как отмечалось и ранее, является задачей анализа, задачей по определению закона движения механической системы под действием заданных внешних сил. При решении этой задачи параметры машинного агрегата и действующие на него внешние силы известны, необходимо определить закон движения: скорости и ускорения в функции времени или обобщенной координаты. Иначе эту задачу можно сформулировать так: заданы управляющие силы и силы внешнего сопротивления, определить обеспечиваемый ими закон движения машины.

Обратная задача - это задача синтеза управления, когда задан требуемый закон движения машины и внешние силы сопротивления, а определяются управляющие силы.

При решении задач динамики используются либо уравнения силового равновесия системы - метод кинетостатики, либо уравнения энергетического равновесия - закон сохранения энергии. Для идеальной механической системы, в которой нет потерь энергии и звенья абсолютно жесткие, этот закон можно применять в виде теоремы об изменении кинетической энергии. Согласно этой теореме работа всех внешних сил действующих на систему расходуется только на изменение ее кинетической энергии. При этом потенциальные силы - силы веса рассматриваются как внешние.

Уравнения движения машинного агрегата в энергетической и дифференциальной форме

Как говорилось ранее, механизм машинного агрегата обычно является многозвенной системой, нагруженной силами и моментами, приложенными к различным ее звеньям. Определение закона движения такой сложной многозвенной системы представляет собой сложную задачу. Как правило, рассматриваемые в этом курсе машинные агрегаты, имеют одну степень свободы. Это значит, что, прежде всего, необходимо определить закон движения всего лишь одного звена, которое будет являться начальным. Заменяем весь сложный многозвенный механизм одним условным звеном – динамической моделью.

Дата добавления: 2014-01-07