Функции частично вычислимые и вычислимые по Маркову

Функция f(x) называется частично определенной на множестве M, если значения этой функции определены не для всех х из M.

Функция f называется арифметической, если ее значения и значения её аргументов являются целыми неотрицательными числами, т.е. область определения аргументов и область значений функции есть множество натуральных чисел.

Положим, как и раньше, алфавит М={1,*}.

Пусть ϕ частично определенная арифметическая функция от n аргументов. Положим, что существует некоторый алгоритм (не обязательно нормальный) A_ϕв алфавите М, позволяющий вычислять значения этой функции всякий раз, когда значение функции существует, т.е. 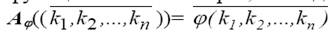тогда и только тогда, когда хотя бы одна из частей этого равенства определена. При этом считаем, что алгоритм A_ϕне применим к словам, отличным от слов вида . Назовем функцию ϕ частично вычислимой по Маркову функцией, если существует нормальный алгоритм B над М, вполне эквивалентный A_ϕотносительно алфавита М.

Иными словами, n-аргументная функция ϕ частично вычислима по Маркову тогда и только тогда, когда существует нормальный алгоритм, позволяющий вычислить значение ϕ(k₁,k₂,...,k_n) для любых совокупностей значений х₁=k₁, х₂=k₂,..., x_n= k_n, при которых ϕ(k₁,k₂,...,k_n) существует.

Если функция определена всюду, т.е. определена для любой совокупности значений своих аргументов, и является частично вычислимой по Маркову, то назовем ее вычислимой по Маркову. Таким образом, n-аргументная функция ϕ вычислима по Маркову тогда и только тогда, когда существует нормальный алгоритм, позволяющий вычислить значение ϕ(x₁,x₂,...,x_n) для любых совокупностей значений x₁,x₂,...,x_n.

Ранее показано, что для всюду определенных арифметических функций

существуют нормальные алгоритмы, вычисляющие их значения (примеры 4, 5). Следовательно, эти функции являются вычислимыми по Маркову.

5. Замыкание, распространение нормального алгоритма

Пусть A - произвольный нормальный алгоритм в алфавите А:

Замыканием алгоритма A называется алгоритм А ^•, полученный из A добавлением формулы подстановки Λ→•Λ в качестве последней подстановки, т.е.

Любой нормальный алгоритм заканчивает процесс переработки слова либо после применения заключительной подстановки, либо если все слова Р₁,Р₂,Р₃,..., Р_nне содержатся в слове, полученном при предыдущем шаге. Подстановка Λ→•Λ применима к любому слову. Следовательно, алгоритм А^•заканчивает переработку слов всегда по заключительной подстановке, которая есть либо некоторая из подстановок P_i→(•)Q_i(1≤ i≤ n) либо Λ→•Λ.

Отметим, что подстановка Λ→•Λ, добавленная к A для получения А^•, стоит последней. Поэтому эта подстановка будет применяться только тогда, когда не применимы все подстановки алгоритма A, причем применение Λ→•Λ к любому слову не изменяет этого слова. Следовательно, результаты применения алгоритмов A и А^• к любому слову в А будут совпадать, т.е. алгоритмы A и А^• вполне эквивалентны.

Пусть A - нормальный алгоритм в алфавите А₁, а алфавит А₂является расширением А₁, т.е. . Тогда можно рассмотреть нормальный алгоритм A^# в алфавите А₂с той же самой схемой, что и A. Очевидно,

, (1)

т.е. A и A^# вполне эквиваленты относительно А₁. Нормальный алгоритм A^# будем называть естественным распространением A на алфавит А₂.

В некоторых случаях удобнее, чтобы алгоритм A^#, удовлетворяющий (1), был не применим к тем словам в А₂, которые не являются словами в А₁. Этого легко достигнуть, приписав к схеме A сверху формулу вида x→x, где x - любая буква из А₂\ А₁. Получившийся нормальный алгоритм называют формальным распространением A на алфавит А₂. Очевидно, что формальное распространение алгоритма A вполне эквивалентно алгоритму A относительно А₁и не применимо к тем словам в А₂, которые не являются словами в А₁.

Использование возможности распространения нормального алгоритма на более широкий алфавит позволяет во многих случаях опускать без особого ущерба точности упоминание об алфавитах, в которых строятся конкретные нормальные алгоритмы.

Дата добавления: 2014-01-07