Маховик и его назначение

Рассмотрим подробно наиболее простой способ регулирования неравномерности вращения - установку дополнительной маховой массы или маховика.

Все звенья механизма обладают инертностью. Как известно из физики, это свойство состоит в том, что чем инертнее материальное тело, тем медленнее происходят изменения его скорости, вызываемые действием приложенных сил. Поэтому, чтобы получить вращение главного вала машины с циклической неравномерностью, не превышающей требуемой величины, инертность этого вала со всеми жестко связанными с ним деталями надо сделать достаточно большой.

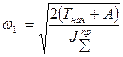
Из уравнения движения машинного агрегата в интегральной форме, очевидно, что, увеличивая инерционность можно уменьшить колебания угловой скорости.

,

где 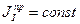, а 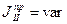. Воздействовать на момент инерции второй группы звеньев сложно, поэтому на практике такое решение не применяется. Поставленная задача решается за счет увеличения момента инерции первой группы звеньев. Для этого на главном валу машины надо закрепить добавочную массу, выполненную в виде колеса с развитым ободом и называемую маховиком. Подбирая его момент инерции, можно обеспечить вращение главного вала машины с заданным коэффициентом неравномерности.

Маховик в машине играет роль аккумулятора кинетической энергии. При разгоне часть положительной работы внешних сил расходуется на увеличение кинетической энергии маховика и скорость, до которой разгоняется система, становится меньше, при торможении маховик отдает запасенную энергию обратно в систему и величина снижения скорости машины уменьшается.

Отсюда можно сделать вывод: чем больше дополнительная маховая масса, тем меньше изменение угловой скорости за цикл и ниже коэффициент неравномерности вращения.

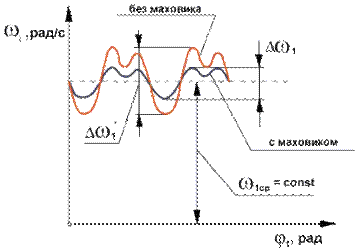
Итак, основное назначение маховика состоит в ограничении колебаний угловой скорости в пределах, устанавливаемых величиной коэффициента неравномерности. Определение момента инерции маховика по заданным условиям движения (т. е. по заданной величине 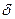) производится в процессе проектирования машины и составляет одну из задач ее динамического синтеза.

Определение приведенного момента инерции первой группы звеньев

Кинетическую энергию исследуемого механизма, также как и момент инерции можно разделить на две части

,

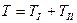где 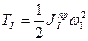, а .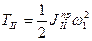

Так как угловая скорость колеблется внутри цикла между значениям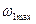и и , то, следовательно, колеблется и кинетическая энергия , проходя через максимальное 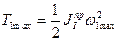и минимальное 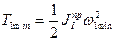значения. Подчеркнем, что момент инерции первой группы звеньев имеет постоянную величину, не зависящую от положения механизма.

Определим наибольший перепад кинетической энергии первой группы звеньев: подставив значения 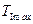и получим

,

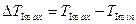С учетом соответствующих значений кинетической энергии:

,

раскроем разность квадратов и умножим и разделим на :

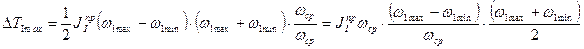
Учитывая, что 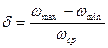, а 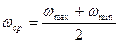, окончательно получим:

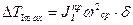
пли, решая относительно искомой величины 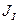, получим формулу для расчета приведенного момента инерции первой группы, который обеспечивает заданный коэффициент неравномерности вращения:

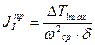
Определение момента инерции дополнительной маховой массы (маховика)

Обозначим за 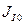момент инерции первой группы звеньев механизма без учета маховика (исходя из рассматриваемого примера – насоса в эту группу звеньев вошли двигатель, редуктор и сам коленчатый вал) – т.е. это момент инерции который непосредственно заложен в конструкции самого машинного агрегата.

Используя приведенную методику, находим 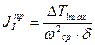, обеспечивающий заданный коэффициент неравномерности вращения.

Далее сравнивая эти инерционные характеристики, решают вопрос о необходимости введения маховика и его размерах.

Если 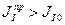, то маховик необходим и 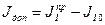- момент инерции дополнительной маховой массы.

Если 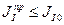, то инерционности конструкции достаточно для обеспечения заданной неравномерности вращения и маховик не требуется.

Решение задачи регулирования хода машины по методу Н.И.Мерцалова.

При расчете маховика (или решении задачи регулирования хода машины) по методу Н.И.Мерцалова задача решается в следующей последовательности:

· Определяются параметры динамической модели, например для ДВС 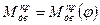- приведенный суммарный момент движущих сил и 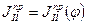- приведенный момент инерции второй группы звеньев.

· Определяется работа движущих сил: т.к. 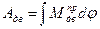, то после построения диаграммы 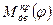, методом графического интегрирования может быть получена диаграмма , конечная ордината которой позволяет получить работу движущих сил за цикл: .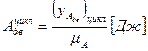

· Основным условием установившегося режима является равенство работ сил движущих и сил полезного сопротивления за цикл. 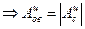, или .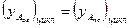

· Из условия, что 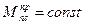, следует 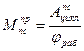где: 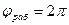– для двухтактного двигателя, 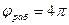– для четырехтактного двигателя. Работу сил полезного сопротивления определяет линейная зависимость 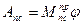, графически ее можно представить в виде прямой линии.

· Исходя из того, что работа суммарная равна алгебраической сумме работ сил движущих и сил полезного сопротивления: 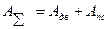, очевидно, что для построения диаграммы 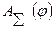необходимо графически сложить ординаты кривой 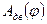и прямой 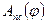, с учетом знака, при этом конечная ордината диаграммы 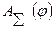должна быть равна нулю, в соответствии с основным условием установившегося режима работы механизма.

· На основании теоремы об изменении кинетической энергии 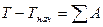, т.е. 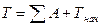. Соответственно, если ось абсцисс графика работы перенести вниз на некую величину 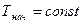, то относительно этой новой оси 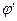график работы и будет выражать изменение за цикл полной кинетической энергии машинного агрегата.

· С другой стороны кинетическую энергию можно разбить на две части 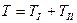. Для нахождения необходимого момента инерции нас интересует кинетическая энергия второй группы звеньев.

· Для построения диаграммы 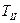воспользуемся выражением , где: 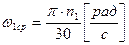. . 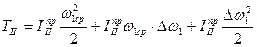Учитывая, что 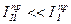и 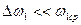, ограничимся членами первого порядка малости, т.е. 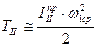. (Первое допущение Мерцалова). Такое допущение позволяет считать диаграмму приведенного момента инерции второй группы звеньев в масштабе 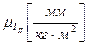диаграммой кинетической энергии второй группы звеньев в масштабе 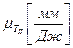. При этом ; 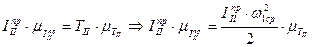, здесь .

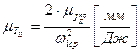· Для получения диаграммы кинетической энергии первой группы звеньев достаточно из полной кинетической энергии машинного агрегата вычесть кинетическую энергию второй группы звеньев. Т.к. 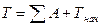, то чтобы вычесть из диаграммы работы диаграмму кинетической энергии второй группы звеньев, необходимо, чтобы эти диаграммы были в одном масштабе 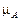, то есть ординаты диаграммы кинетической энергии второй группы звеньев должны быть пересчитаны по формуле: .

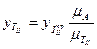· Далее на полученном графике определяют положение 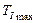и 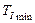, для того, чтобы показать 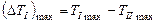. Рассчитав 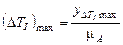, можно определить момент инерции первой группы звеньев.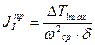

Из этого выражения, определив предварительно 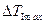, можно решить две задачи:

• задачу синтеза - при заданном 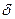определить необходимый для его обеспечения приведенный момент инерции 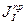и решить вопрос о наличии маховика.
• задачу анализа - при заданном 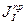определить обеспечиваемый им коэффициент неравномерности .

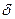Определение закона движения начального звена механизма при установившемся режиме движения

При определении закона движения начального звена механизма используют соотношение

.

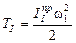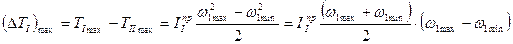
так как 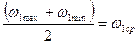, а ,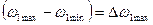

то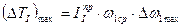

Откуда следует, что при принятых допущениях изменение угловой скорости начального звена пропорционально изменению кинетической энергии первой группы звеньев, то есть максимальному приращению кинетической энергии 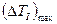будет соответствовать максимальное приращение угловой скорости начального звена 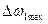, так как .

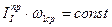В связи с этим построенная диаграмма кинетической энергии первой группы звеньев может являться и графиком угловой скорости, если принять равенство соответствующих ординат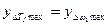

и пересчитать масштабы ,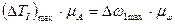

тогда с учетом того, что 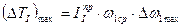масштаб .

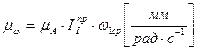Через середину отрезка 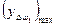проводят линию средней угловой скорости, значение которой определяется как

, .

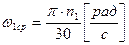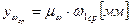Графическую величину 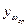откладывают от положения средней линии, и получают положение оси 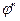, относительно которой график будет изображать изменение угловой скорости начального звена за один цикл установившегося режима движения. Этот график позволяет найти и 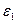для любого положения начального звена .

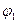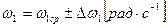, где: .

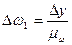А угловое ускорение можно найти, например, графическим методом:

,

,

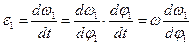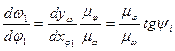где 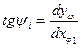тангенс угла наклона касательной в каждой точке графика 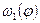, значение производной подставляются в исходное уравнение с учетом знака.

Дата добавления: 2014-01-07