Лекция №7 назначение показателей надежности элементов из условия обеспечения максимальной вероятности безотказной работы систем при ограниченных средствах на ее создание

Вероятность безотказной работы системы, состоящей из n элементов с интенсивностями отказов λ_i, в течение времени t равняется

(4.29)

Из этого выражения видно, что максимальное значение р(t) достигается при минимальном значении (значение t будут влиять только на численное значение оптимума).

Стоимость (материальные затраты на производство) i-го элемента системы зависит от λ_i и может быть представлена в виде

; (4.30)

где К_i , К_λi – известные положительные числа.

При проектировании системы может стоять задача о назначении таких значений λ_i, чтобы

при условии 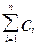< С, где С – материальные средства выделенные на создание системы.

Подставляя (4.30) в (4.29), получаем

p(t)=exp. (4.31)

где a_i=k_ik_λi; b=c_ik_i, то есть b_i=f(c_i).

Таким образом, с учетом (4.31), математическая формулировка указанной задачи приобретает вид: необходимо найти такие b_i(i=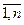), а соответственно и λ_i, чтобы функция

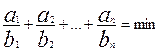(4.32)

в области b₁+b₂+b₃+…+b_n=B, b_i>0.

В=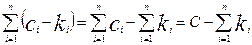 (4.33)

Пусть n = 4, то есть система состоит из четырех элементов. Введем обозначения: b₁+b₂+b₃+b₄=B; b₁+b₂=B₂; b₁=B₁. Аналогично предыдущей лекции, с учетом (4.32), получим последовательность минимизируемых функций:

(4.34)

(4.35)

(4.36)

(4.37)

Соотношения (4.34) — (4.37) представляют собой описание многошаговой процедуры распределения материальных средств между элементами системы и обеспечивает выполнение условия (4.32).

Найдем сначала (как в предыдущей лекции) условное оптимальное распределение на всех шагах, то есть «пройдем» весь процесс от конца к началу. Подставим (4.37) в (4.36) и из условия минимального значения выражения в квадратных скобках найдем условно оптимальное значение b₂ и соответствующее ему значение функции f₂(B₂):

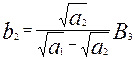
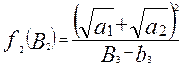(4.38)

Повторением процедуры после подстановки (4.38) в (4.35) находим

(4.39)

Наконец, подставив (4.39) в (4.34), определяем оптимальное (уже не условное) значение b₄:

(4.40)

Для системы из n элементов, после подстановки (4.30) и (4.31) в (4.40), получаем

Отсюда

, i=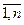 (4.41)

При определении λ_iопт по формуле (4.41) находится максимальное значение вероятности безотказной работы системы, которое можно обеспечить, вложив в разработку системы средства С.

Аналогично может быть решена задача назначения элементов системы для обеспечения заданного значения [p(t)]_зад вероятности безотказной работы при минимуме материальных затрат на ее создание.

После логарифмирования (4.29) имеем

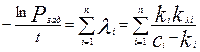
Заданное значение p(t) необходимо обеспечить при минимальном значении

, то есть при

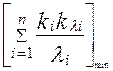
Тогда

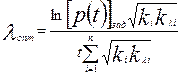(4.42)

При этом затраты на создание системы минимальны и определяются выражением

(4.43)

Выражение (4.43) позволяет определить минимальные затраты на разработку и изготовление системы, которая обеспечивает заданный уровень безотказной работы в течение времени t.

Дата добавления: 2014-01-07