А. Общее пассивное резервирование

Пассивное резервирование с неизменным нагружением

Особенности невосстанавливаемых систем с пассивным резервированием

При пассивном резервировании с неизменным нагружением элементы находятся в одинаковых условиях, которые не изменяются и после возникновения отказа. Рассмотрим два типа соединения элементов в резервных системах: общее и раздельное.

При общем резервировании резервируется система в целом. Основным параметром резервирования является его кратность, то есть отношение числа, резервных элементов к числу элементов основных.

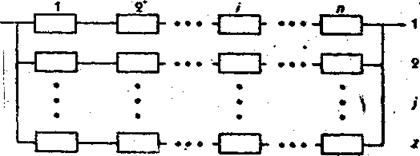
На рис. 5.1 представлена резервированная система: основная система состоит из n последовательно соединенных элементов, параллельно ему включены (z-1) резервных систем, аналогичных основной системе. Все системы имеют одинаковое нагружение.

Рис.5.1 Схема резервированной системы при пассивном резервировании

Будем считать, что все элементы одной системы имеют различную надежность, а одноименные элементы всех систем (основной и резервный) - равнонадежны.

На основании теоремы умножения вероятностей независимых событий вероятность безотказной работы любой системы в течение времени t

P_c(t)=p₁(t)p₂(t)…p_i(t)…p_n(t)=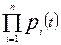 (5.1)

где p_i(t)— вероятность безотказной работы i -го элемента системы в течение времени t.

При известных интенсивностях отказов элементов

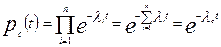
где - интенсивность отказов одной из z систем.

Очевидно, что интенсивность отказов одной из систем

.

На основании теоремы о вероятности появления хотя бы одного из независимых событий имеем для резервированной системы с общим резервированием: вероятность отказа всех z систем (всей системы)

(5.2)

вероятность безотказной работы всей системы:

(5.3)

дифференциальная функция распределения вероятностей (плотности вероятности) времени безотказной работы (наработки до отказа):

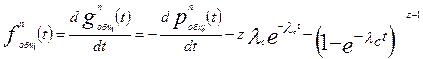(5.4)

интенсивность отказов резервной системы:

(5.5)

Так как λ_сt<<1, то , а так как (λ_ct)→0?

То (5.6)

Следовательно, даже если интенсивности отказов элементов и отдельных систем постоянные величины, то интенсивность отказов резервной системы является функцией времени (наработки) и тем сильнее зависит от времени, чем выше кратность резервирования z.

Применяя к (5.5) правило Лопиталя, можно, показать, что при t→∞ 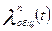→λ_c, то есть интенсивность отказов резервированной системы приближается к своей границе — значению интенсивности отказов системы нерезервированной. Среднее время безотказной работы резервированной системы (средняя наработка до отказа) есть математическое ожидание наработки до отказа. Как следует из определения математического ожидания непрерывной случайной величины, величину Т_ср.общ можно определить следующим образом:

(5.7)

Интегрируя (5.7) по частям, получаем:

(5.8)

Тогда

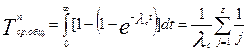(5.9)

Все приведенные формулы справедливы для случая, когда отказ резервированной системы соответствует отказу всех параллельно включенных систем.

Б. Раздельное пассивное резервирование

При раздельном резервировании системы, состоящей из последовательно соединенных элементов, каждый элемент имеет (z_i1) параллельно подключенных резервных элементов (рис. 5.2).

Общая система, таким образом, представляет собой последовательное соединение n блоков (узлов), каждый из которых состоит из z_i элементов, соединенных параллельно.

Вероятность безотказной работы общей системы в течение времени t

(5.10)

где р_Бi(t) — вероятность безотказной работы i-го блока в течение времени t;

g_Бi(t) = [g_i(t)]^Zi — вероятность отказа i-гo блока в течение времени t;

q_i(t) - вероятность отказа элемента в i-м блоке (все элементы блока равнонадежны).

1 2 i n

……. ….

::::

z₁ z₂ z_i z_n

Рис. 5.2 Схема с раздельным пассивным резервированием

При показательном законе распределения временибезотказной работы (наработки до отказа) и постоянной интенсивности отказов элементов (λ_i = const) имеем

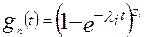; (5.11)

Тогда

(5.12)

Определим интенсивность отказов системы с раздельным пассивным резервированием. Для каждого (i-го) блока с параллельным соединением элементов имеем:

вероятность безотказной работы:

(5.13)

вероятность отказа:

(5.14)

плотность вероятности времени безотказной работы:

(5.15)

интенсивность отказов:

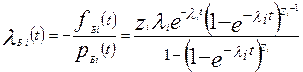(5.16)

Тогда интенсивность отказов всей системы

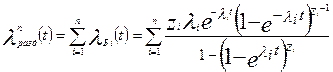(5.17)

Обычно для отдельного элемента справедливо λ_it<<1, тогда

(5.18)

То есть, приняв (λ_it)^Zi≈0, имеем

(5.19)

Следовательно, интенсивность отказов системы с раздельным резервированием также является функцией времени.

Если все элементы системы равнонадежны

P₁=p₂=p₃=…=p_i=…=p_n=p, g=1p

а все блоки имеют одинаковую кратность резервирования

z₁=z₂=…=z_j=…=z_n=z, то

^Х (5.20)

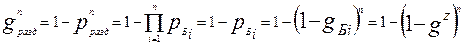(5.21)

разложив (1g)ⁿ и (1g^z)ⁿ в ряды

и ограничившись двумя первыми членами ряда, имеем

g_общⁿ≈n^zg^z; g_раздⁿ=ng^z (5.22)

Таким образом, раздельное резервирование в сравнении с общим резервированием даст выигрыш в надежности, определяемый отношением

Дата добавления: 2014-01-07