Первое начало термодинамики

Термодинамическая система находится в состоянии равновесия, если описывающие её макроскопические параметры не меняются с течением времени. Термодинамический процесс называется квазистатическим, если переход из одного состояние в другое происходит медленно, а каждое состояние системы можно считать равновесным.

О справедливости закона сохранения энергии можно утверждать, если сохранение энергии имеет место при переходе энергии из одной формы в другую. Именно это факт был доказан в первом начале термодинамики, впервые сформулированном Р.Клаузиусом (1822 – 1888), немецким физиком и математиком (рис.7.4), в 1854 году.

Он формулируется следующим образом: количество теплоты, полученное системой, идет на приращение ее внутренней энергии и на совершение системой работы против внешних сил:

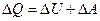, (7.3.1)

или в дифференциальной форме:

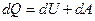(7.3.2)

Рис.7.4. Рудольф Клаузиус.

Экспериментально, как уже отмечалось, связь между механической и тепловой энергией (механический эквивалент теплоты) была установлена в опытах Джоуля[2].

Первое начало термодинамики представляет собой закон сохранения механической и тепловой энергии при их взаимопревращениях. Отсюда стало понятно, что закон сохранения энергии должен носить всеобщий характер, сохраняясь при переходах энергии из одной формы в другую для всех видов энергий. Последующее развитие физики успешно подтвердило этот вывод экспериментально на атомном и ядерном уровнях, во всех взаимопревращениях элементарных частиц.

Одним из следствий первого начала термодинамики является утверждение, что количество теплоты, поглощаемое или выделяемое системой, зависит от пути перехода из одного состояния в другое. Рассмотрим действие первого начала термодинамики на некоторых изопроцессах.

В изотермическом процессе, когда температура постоянна (Т=const), изменения внутренней энергии не происходит (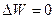) и, следовательно, передача некоторой системе тепла полностью расходуется на совершение работы 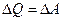. Работа, совершаемая в этом процессе, вычисляется по РV - диаграмме как заштрихованная площадь под кривой (рис. 7.5):

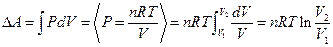, (7.3.3)

где 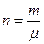- число молей газа.

В изохорическом процессе, когда постоянен объем (V=const), механическая работа не совершается, так как 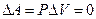. Поэтому изменение внутренней энергии тела равно количеству переданной ему теплоты:

.

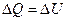Отсюда следует, что при любых процессах, происходящих в замкнутой системе, когда 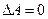, внутренняя энергия остается неизменной.

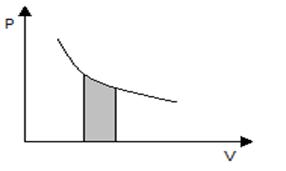
Рис.7.5. Вычисление работы, совершенной газом, в

изотермическом процессе.

В изобарическом процессе, когда постоянно давление (Р=const), тепло расходуется на изменение внутренней энергии (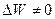), причем система совершает работу ():

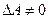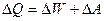(7.3.4)

Пример 7.1. Установить связь между теплоемкостью при постоянном давлении с_р и объеме с_v. Если передача теплоты происходит при постоянном давлении, то удельную теплоемкость обозначают с_р, если при постоянном объеме – с_v.

В соотношении (7.3.4.) передача теплоты и изменение внутренней энергии системы при постоянном давлении и объеме описываются соответственно выражениями:

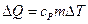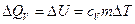, . (7.3.5)

где 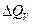- передача тепла при постоянном объеме.

Для вычисления совершенной работы воспользуемся уравнением Клапейрона – Менделеева (6.4.7):

.

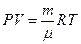Из него получим выражение для изменения работы :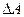

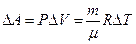. (7.3.6)

Подставляя (7.3.5) и (7.3.6) в (7.3.4) получим:

.

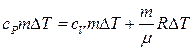Откуда для вещества с молекулярной массой µ различие теплоемкостей при постоянном давлении и объеме составляет:

,

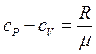А для одного моля газа это выражение имеет вид:

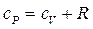. (7.3.7)

Адиабатический процесс происходит без изменения количества теплоты, поступающей в систему и отданной ею 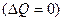. Получим формулу, описывающую аналитически адиабатический процесс.

Для идеального газа это выражение вычисляется из первого начала термодинамики:

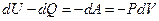. (7.3.8)

Учитывая, что при постоянном объеме :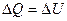

,

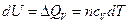уравнение (7.3.8) запишем в виде:

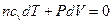(7.3.9)

Дифференцируя соотношение:

,

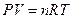получим

.

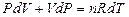Выражая отсюда dT и подставляя в уравнение (7.3.9), получаем:

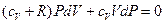(7.3.10)

Учитывая (7.3.7), уравнение (7.3.10) принимает вид:

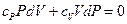. (7.3.11)

Обозначим .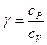

Уравнение (7.3.11) можем записать в виде:

.

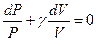Откуда, интегрируя предыдущее выражение, получим:

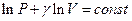. (7.3.9)

Таким образом, при адиабатическом расширении (сжатии) идеального газа выполняется соотношение:

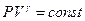. (7.3.10)

Адиабатический процесс представлен на (рис.7.6). Примером такого процесса может служить быстрое накачивание насосом футбольного мяча. Если скорость движения поршня велика, то вся совершенная работа переходит во внутреннюю энергию газа в камере мяча. Нагреванием насоса можно пренебречь.

Пример.7.2. Рассчитать отношение теплоемкостей при постоянном давлении и объеме для одноатомного идеального газа.

Рассмотрим процесс при постоянном объеме: 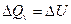. Внутренняя энергия n молей одноатомного идеального газа – это суммарная кинетическая энергия его молекул, которая составляет:

,

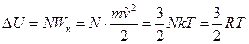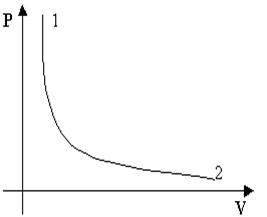
Рис.7.6. Адиабатический процесс.

а для потока тепла при постоянном объеме, справедливо соотношение (7.3.5):

.

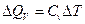Откуда, используя соотношение (7.3.7), для идеального одноатомного газа теплоемкость при постоянном объеме, составляет:

,

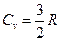а при постоянном давлении:

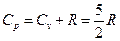
Коэффициент 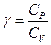в выражении для адиабатического процесса 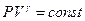для одноатомного идеального газа составляет:

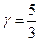
Дата добавления: 2014-01-07