Замена переменных в двойном интеграле. Двойной интеграл в полярных координатах

16.1.5.1.Теорема о замене переменных в двойном интеграле. Пусть на плоскости Ouv задана область G, и пусть отображение 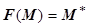преобразует эту область в область D на плоскости Oxy. Будем считать, что отображение F задаётся функциями 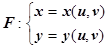. Пусть: 1). F взаимно однозначно отображает G на D; 2). функции x ( u,v ), y ( u,v ) непрерывно дифференцируемы на G (имеют непрерывные частные производные); 3). якобиан не обращается в нуль на G. Докажем, что в этих предположениях .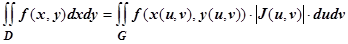

Док-во. 1. Рассмотрим, как связаны между собой площадь параллелограмма АВСЕ со сторонами 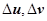в области G и площадь его образа при преобразовании F -криволинейного параллелограмма 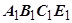в области D. С точностью до бесконечно малых высших порядков по сравнению с 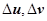, площадь криволинейного параллелограмма 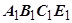равна площади обычного параллелограмма, построенного на векторах 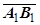и 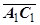. Пусть точка А имеет координаты (u,v ), тогда точка А ₁ будет иметь координаты ( x ( u,v ), y ( u,v )), т.е. 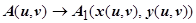. Для других точек: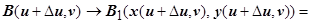 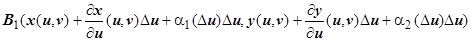(по формуле приращения дифференцируемой функции). Аналогично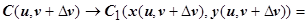

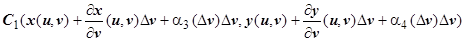, где 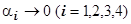при 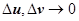. Пренебрежём членами порядка малости выше первого по сравнению с 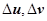. Тогда .

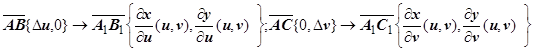Пусть теперь i,j,k - базисные орты пространства, в котором лежит плоскость Oxy. Как известно, площадь параллелограмма, построенного на векторах 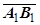и 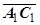, равна модулю векторного произведения этих векторов (проекции на орт k равны нулю):

.

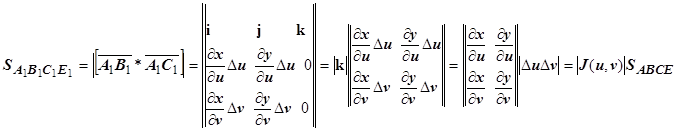Мы доказали замечательную вещь. Если вокруг точки 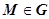взять маленькую область, то после преобразования F площадь этой области меняется в 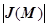раз.

2. Перейдём к доказательству основной формулы. Разобьём G прямыми, параллельными осям координат, на области 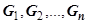. Образы этих линий дадут разбиение D на области 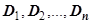. Для этого 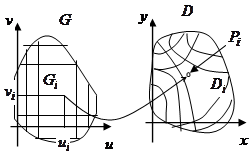разбиения составим интегральную cумму 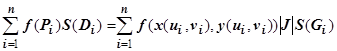. Устремим 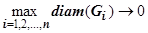; тогда и 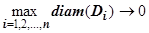. И слева, и справа интегральные суммы записаны для непрерывных функций, следовательно,и слева, и справа существуют пределы - двойные интегралы, и они равны: 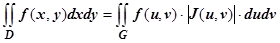, что и требовалось доказать.

16.1.5.2. Двойной интеграл в полярных координатах. Нам придётся применять эту формулу, в основном, для перехода к полярным координатам. Роль переменных u и v будут играть r и 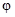. Как известно, 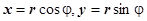. Вычислим якобиан: 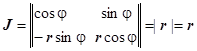, следовательно, 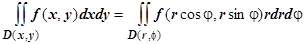. Двойной интеграл в координатах r, 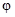вычисляется также как и в координатах x, y, переходом к двухкратному, при этом внешний обычно берут по 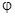. Если область D описывается как , то 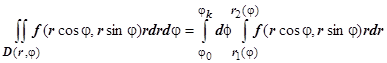. Естественно, если 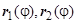- кусочные функции, то внешний интеграл разбивается на несколько слагаемых. Однозначно дать рецепт, когда имеет смысл переходить к полярным координатам, нельзя, это дело опыта. Можно пробовать перейти к r, 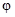, если либо f (x, y ), либо кривые, ограничивающие область интегрирования, либо и то, и другое вместе, зависят от комбинации .

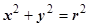Если 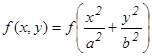и/или область D ограничивается эллипсом 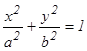, полезны обобщённые полярные координаты 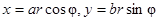. Каков якобиан этого преобразования?

Дата добавления: 2014-01-07