
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Поверхностный интеграл второго рода (по координатам)
|
|
|
|
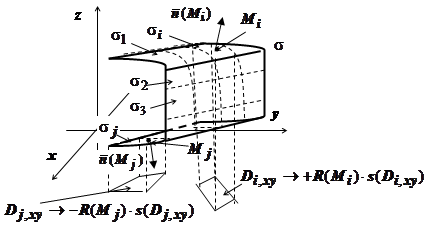 16.4.4.1. Определение поверхностного интеграла второго рода. Пусть в пространстве переменных x,y,z задана ограниченная кусочно-гладкая двусторонняя поверхность
16.4.4.1. Определение поверхностного интеграла второго рода. Пусть в пространстве переменных x,y,z задана ограниченная кусочно-гладкая двусторонняя поверхность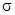 , на которой введена ориентация (т.е. с помощью единичного вектора нормали в какой-либо точке
, на которой введена ориентация (т.е. с помощью единичного вектора нормали в какой-либо точке 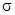 задана сторона поверхности), и на которой определена функция R (x, y, z).Разобьём поверхность на
задана сторона поверхности), и на которой определена функция R (x, y, z).Разобьём поверхность на 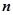 частей
частей 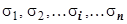 , на каждой из частей
, на каждой из частей  выберем произвольную точку
выберем произвольную точку 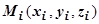 , найдём
, найдём  , нормаль
, нормаль 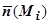 в точке
в точке 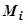 к выбранной стороне поверхности, и площадь
к выбранной стороне поверхности, и площадь 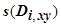 проекции части
проекции части  на плоскость ОХУ. В интегральную сумму слагаемое
на плоскость ОХУ. В интегральную сумму слагаемое 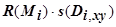 возьмём со знаком "+", если
возьмём со знаком "+", если 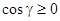 (т.е. если угол
(т.е. если угол  между
между 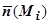 и осью Oz - острый; проекция
и осью Oz - острый; проекция 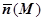 на орт
на орт 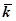 оси Oz положительна), и со знаком "-", если
оси Oz положительна), и со знаком "-", если 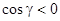 . В результате интегральная сумма будет иметь вид
. В результате интегральная сумма будет иметь вид 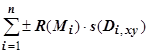 . Если существует предел последовательности интегральных сумм при
. Если существует предел последовательности интегральных сумм при 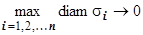 , не зависящий ни от способа разбиения поверхности
, не зависящий ни от способа разбиения поверхности 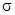 на части
на части 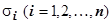 , ни от выбора точек
, ни от выбора точек 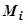 , то функция R (x, y, z) называется интегрируемой по поверхности
, то функция R (x, y, z) называется интегрируемой по поверхности 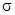 , а значение этого предела называется поверхностным интегралом второго рода, или поверхностным интегралом по координатам х, у, и обозначается
, а значение этого предела называется поверхностным интегралом второго рода, или поверхностным интегралом по координатам х, у, и обозначается 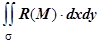 .
.
Теорема существования. Если функция R (x, y, z) непрерывна на поверхности 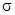 , то она интегрируема по этой поверхности.
, то она интегрируема по этой поверхности.
Если на поверхности 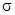 , вместе с функцией R (x, y, z), определены функции P (x, y, z) и Q (x, y, z), то, так же, как и интеграл
, вместе с функцией R (x, y, z), определены функции P (x, y, z) и Q (x, y, z), то, так же, как и интеграл 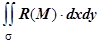 , определяются интегралы
, определяются интегралы  и
и 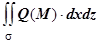 ; в приложениях, как мы видели из рассмотренной в начале раздела физической задачи, обычно рассматривается сумма этих интегралов, которая обозначается
; в приложениях, как мы видели из рассмотренной в начале раздела физической задачи, обычно рассматривается сумма этих интегралов, которая обозначается  .
.
 16.4.4.2. Свойства поверхностного интеграла второго рода. Для этого интеграла, как и для криволинейного интеграла второго рода, имеет смысл формулировать следующие свойства: линейность, аддитивность и зависимость поверхностного интеграла от выбора стороны поверхности: при изменении ориентации поверхности интеграл меняет знак.
16.4.4.2. Свойства поверхностного интеграла второго рода. Для этого интеграла, как и для криволинейного интеграла второго рода, имеет смысл формулировать следующие свойства: линейность, аддитивность и зависимость поверхностного интеграла от выбора стороны поверхности: при изменении ориентации поверхности интеграл меняет знак.
16.4.4.3. Вычисление поверхностного интеграла второго рода. Пустьповерхность 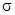 взаимно однозначно проецируется в область
взаимно однозначно проецируется в область  на плоскости Оху. В этом случае
на плоскости Оху. В этом случае 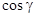 имеет одинаковый знак во всех точках поверхности. Именно,
имеет одинаковый знак во всех точках поверхности. Именно, 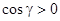 , если рассматривается верхняя сторона поверхности, и
, если рассматривается верхняя сторона поверхности, и 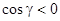 , если рассматривается нижняя сторона. Поэтому для верхней стороны все слагаемые в интегральной сумме должны браться со знаком "+", и сумма будет иметь вид
, если рассматривается нижняя сторона. Поэтому для верхней стороны все слагаемые в интегральной сумме должны браться со знаком "+", и сумма будет иметь вид  . Если поверхность задана уравнением
. Если поверхность задана уравнением  ,
, 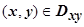 , то эта сумма равна
, то эта сумма равна  . В последней сумме легко увидеть интегральную сумму для двойного интеграла
. В последней сумме легко увидеть интегральную сумму для двойного интеграла  . Переход к пределу при
. Переход к пределу при 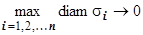 (при этом и
(при этом и 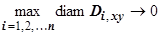 ) даст
) даст
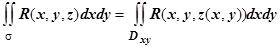 . Напомню, что эта формула получена для верхней стороны поверхности. Если выбрана нижняя сторона, то все слагаемые в интегральной сумме должны браться со знаком "-", и интегральная сумма будет иметь вид
. Напомню, что эта формула получена для верхней стороны поверхности. Если выбрана нижняя сторона, то все слагаемые в интегральной сумме должны браться со знаком "-", и интегральная сумма будет иметь вид  . Рассуждая, как и для верхней стороны, получим, что в этом случае
. Рассуждая, как и для верхней стороны, получим, что в этом случае 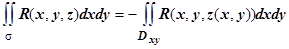 . Окончательно,
. Окончательно,  , где знак "+" берётся для верхней стороны поверхности, знак "-" - для нижней стороны.
, где знак "+" берётся для верхней стороны поверхности, знак "-" - для нижней стороны.
Аналогично изложенному, для других интегралов: 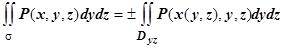 , если поверхность однозначно проецируется в область
, если поверхность однозначно проецируется в область  на плоскости Oyz, при этом знак "+" берётся для "передней" стороны поверхности (где
на плоскости Oyz, при этом знак "+" берётся для "передней" стороны поверхности (где  ), для "задней" стороны, где
), для "задней" стороны, где 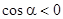 , берётся знак "-";
, берётся знак "-";  , если поверхность однозначно проецируется в область
, если поверхность однозначно проецируется в область  на плоскость Oхz, знак "+" берётся для "правой" стороны поверхности (где
на плоскость Oхz, знак "+" берётся для "правой" стороны поверхности (где  ), для "левой" стороны, где
), для "левой" стороны, где 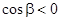 , берётся знак "-". Как и для поверхностного интеграла первого рода, если проецирование не взаимно однозначно, поверхность разбивается на части, которые проецируются однозначно.
, берётся знак "-". Как и для поверхностного интеграла первого рода, если проецирование не взаимно однозначно, поверхность разбивается на части, которые проецируются однозначно.
 Примеры. 1. Вычислить
Примеры. 1. Вычислить 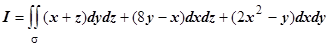 , s - часть поверхности цилиндра y =
, s - часть поверхности цилиндра y =  , заключенная между плоскостями x =0, x =8, z =0, z =3. Сторона поверхности выбирается так, чтобы нормаль образовывала острый угол с осью Oх.
, заключенная между плоскостями x =0, x =8, z =0, z =3. Сторона поверхности выбирается так, чтобы нормаль образовывала острый угол с осью Oх.
Решение: Определяем знаки направляющих косинусов нормали cosa>0, cosb<0, cosg=0. Поэтому

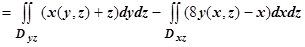 , где
, где
Dyz ={(y, z): 0£ y £16, 0 £ z £ 3}, Dxz ={(x, z): 0 £ x £ 8, 0 £ z £ 3} - проекции s на плоскости Oyz и Oxz соответственно. Проекция поверхности s на плоскость Oxy вырождается в линию - параболу y = , cosg=0, поэтому интеграл по Dxy в данном случае отсутствует. Вычислим отдельно интегралы по Dyz и Dxz , выражая x (y, z) и y (x, z) из уравнения поверхности s: x (y, z)=2
, cosg=0, поэтому интеграл по Dxy в данном случае отсутствует. Вычислим отдельно интегралы по Dyz и Dxz , выражая x (y, z) и y (x, z) из уравнения поверхности s: x (y, z)=2 , y (x, z)=
, y (x, z)= .
.
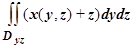 =
=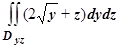 =
= dy =328,
dy =328, =
=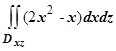 =
=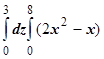 dx =928. Окончательно I = 328 - 928 = - 600.
dx =928. Окончательно I = 328 - 928 = - 600.
2. Вычислить  , где s - часть плоскости
, где s - часть плоскости 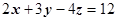 , ограниченная координатными плоскостями x =0, у =0, z =0. Сторона поверхности выбирается так, чтобы нормаль образовывала острый угол с осью Oz.
, ограниченная координатными плоскостями x =0, у =0, z =0. Сторона поверхности выбирается так, чтобы нормаль образовывала острый угол с осью Oz.
Решение. Из двух направлений нормали к s 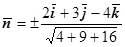 мы должны выбрать такое, для которого коэффициент при орте
мы должны выбрать такое, для которого коэффициент при орте 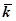 (т.е.
(т.е. 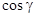 ) положителен, поэтому выбираем знак "-", тогда
) положителен, поэтому выбираем знак "-", тогда 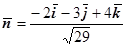 . В соответствии со знаками направляющих косинусов,
. В соответствии со знаками направляющих косинусов, 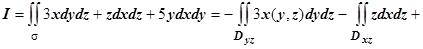
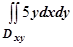 . Вычисляем эти интегралы.
. Вычисляем эти интегралы.
1. 

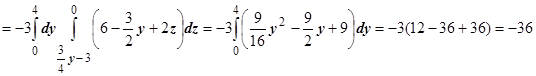 .
.
2. 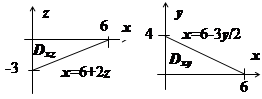
 .
.
3. 
 . Окончательно,
. Окончательно, 
В заключение напомню, что вычисление поверхностного интеграла второго рода всегда можно свести к вычислению поверхностного интеграла первого рода. Так, в последнем примере подынтегральное выражение равно  , где
, где 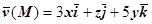 ,
, 
 . Поэтому
. Поэтому  , и, проектируя s на плоскость Оху
, и, проектируя s на плоскость Оху  , получим
, получим 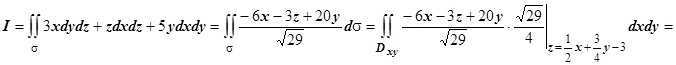
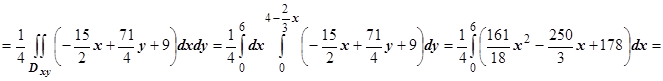
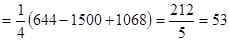 .
.
17. Теория поля.
17.1. Скалярное поле.
 17.1.1. Скалярное поле, производная по направлению, градиент. Все физические процессы, проходящие в любой области пространства, характеризуются определёнными значениями некоторых величин. Так, нагревание тела описывается изменением температуры в точках этого тела; загнивание экономического региона характеризуется количеством остановленных в нём предприятий и т.д. Если каждой точке М некоторой области V пространства соответствует значение некоторой скалярной величины u (M), то говорят, что в области V задано скалярное поле u (M). Поле называется стационарным, если оно не меняется во времени; мы будем изучать только стационарные поля.
17.1.1. Скалярное поле, производная по направлению, градиент. Все физические процессы, проходящие в любой области пространства, характеризуются определёнными значениями некоторых величин. Так, нагревание тела описывается изменением температуры в точках этого тела; загнивание экономического региона характеризуется количеством остановленных в нём предприятий и т.д. Если каждой точке М некоторой области V пространства соответствует значение некоторой скалярной величины u (M), то говорят, что в области V задано скалярное поле u (M). Поле называется стационарным, если оно не меняется во времени; мы будем изучать только стационарные поля.
Формально определение скалярного поля совпадает с определением функции u (M), заданной в области V; это верно и по существу, однако при изучении теории поля полезно иметь в виду, что функция u (M) описывает конкретную физическую реальность. Для изучения функциональной зависимости u (M) нам придётся ввести некоторую систему координат. Вид функции u (M) (её аналитическое выражение) меняется в зависимости от того, как введена координатная система (где расположено начало системы координат, куда направлены оси, каков масштаб измерения расстояний и т.д.), однако сущность, которую описывают эти разные выражения, одна и та же. Произвол в задании системы координат приводит к необходимости различать величины, не зависящие от конкретной системы (инвариантные относительно системы координат), и величины, принимающие разные значения в разных системах (неинвариантные величины). Основной инвариантной величиной является, конечно, само значение u (M) поля в точке М. Мы будем называть поле u (M) гладким, если функция u (M) имеет непрерывные частные производные 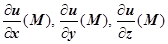 . Значения этих производных в точке М зависят от системы координат, однако составленная с их помощью линейная комбинация базисных ортов системы
. Значения этих производных в точке М зависят от системы координат, однако составленная с их помощью линейная комбинация базисных ортов системы  образует градиент поля u (M) и инвариантна относительно системы координат. Вектор
образует градиент поля u (M) и инвариантна относительно системы координат. Вектор 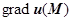 направлен в сторону роста значений поля u (M) по направлению наибольшей скорости роста; длина
направлен в сторону роста значений поля u (M) по направлению наибольшей скорости роста; длина 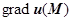 равна скорости роста в этом направлении. Инвариантна относительно системы координат производная поля в точке М по любому направлению
равна скорости роста в этом направлении. Инвариантна относительно системы координат производная поля в точке М по любому направлению  , выходящему из этой точки, так как она характеризует скорость изменения поля в направлении
, выходящему из этой точки, так как она характеризует скорость изменения поля в направлении  . Формально производная по направлению определяется как
. Формально производная по направлению определяется как 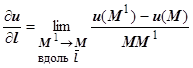 , где
, где 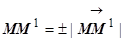 в зависимости от того, имеют ли ось
в зависимости от того, имеют ли ось  и вектор
и вектор  одинаковые или противоположные направления. Производная по направлению выражается через градиент формулой
одинаковые или противоположные направления. Производная по направлению выражается через градиент формулой
 ,
,
где 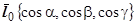 - орт направления
- орт направления  ,
,  - направляющие косинусы этого направления.
- направляющие косинусы этого направления.
В дальнейшем для обозначения градиента мы часто будем применять введённый Гамильтоном оператор 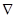 ("набла"). Этот вектор-оператор определяется как
("набла"). Этот вектор-оператор определяется как  . Если формальное произведение
. Если формальное произведение  понимать как
понимать как 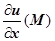 , то
, то 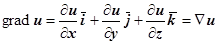 , т.е. произведение вектора набла на скаляр u (M) даёт значение градиента поля u в точке M.
, т.е. произведение вектора набла на скаляр u (M) даёт значение градиента поля u в точке M.
Градиент поля имеет следующие дифференциальные свойства
1. 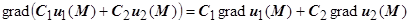 , или
, или 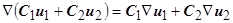 ;
;
2.  , или
, или 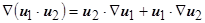 ;
;
3.  , или
, или  ;
;
4. 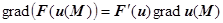 , или
, или 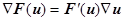 ,
,
которые легко доказываются применением обычных правил дифференцирования.
Для визуального изображения скалярных полей применяются поверхности и линии (в плоском случае) уровня. Поверхностью уровня скалярного поля u (M), соответствующей значению поля С, называется геометрическое место точек 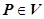 таких, что
таких, что  . Поверхности уровня, соответствующие разным значениям постоянной С, не могут иметь общих точек, поэтому область V, в которой задано поле, расслаивается на поверхности уровня; совокупность этих поверхностей, построенных для некоторого регулярного набора значений С, например, С =1, С =2, С =3 и т.д., даёт наглядное представление об изменении поля при переходе от одной точке к другой. Поле меняется быстрее там, где эти поверхности расположены гуще. Градиент поля в каждой точке Р 0 ортогонален поверхности уровня, проходящей через эту точку, т.е. поверхности
. Поверхности уровня, соответствующие разным значениям постоянной С, не могут иметь общих точек, поэтому область V, в которой задано поле, расслаивается на поверхности уровня; совокупность этих поверхностей, построенных для некоторого регулярного набора значений С, например, С =1, С =2, С =3 и т.д., даёт наглядное представление об изменении поля при переходе от одной точке к другой. Поле меняется быстрее там, где эти поверхности расположены гуще. Градиент поля в каждой точке Р 0 ортогонален поверхности уровня, проходящей через эту точку, т.е. поверхности 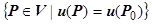 .
.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1637; Нарушение авторских прав?; Мы поможем в написании вашей работы!