
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Частные случаи векторных полей
|
|
|
|
.
Векторное поле называется однородным (или постоянным), если 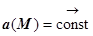 .
.
Векторное поле называется плоским, если все векторы 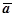 (M) параллельны некоторой плоскости П и одинаковы вдоль каждого перпендикуляра к П. Если система координат введена так, что П совпадает с плоскостью Оху, то, очевидно,
(M) параллельны некоторой плоскости П и одинаковы вдоль каждого перпендикуляра к П. Если система координат введена так, что П совпадает с плоскостью Оху, то, очевидно, 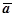 (M)
(M)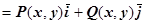 . Плоское поле достаточно рассматривать в пределах плоскости Оху, так как во всех плоскостях, параллельных Оху, оно одинаково. Для плоского поля
. Плоское поле достаточно рассматривать в пределах плоскости Оху, так как во всех плоскостях, параллельных Оху, оно одинаково. Для плоского поля 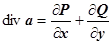 ,
, 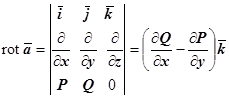 . Пример плоского поля - магнитное поле, создаваемое током I, текущим по бесконечно длинному проводнику. Если ось Oz направлена вдоль этого проводника, то вектор напряженности магнитного поля равен
. Пример плоского поля - магнитное поле, создаваемое током I, текущим по бесконечно длинному проводнику. Если ось Oz направлена вдоль этого проводника, то вектор напряженности магнитного поля равен 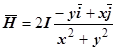 , это поле определено везде, кроме оси Oz.
, это поле определено везде, кроме оси Oz.
Векторное поле называется центральным, если в каждой точке 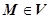 вектор
вектор 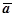 (M) коллинеарен радиусу-вектору этой точки:
(M) коллинеарен радиусу-вектору этой точки: 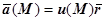 (
(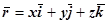 ). Так как
). Так как 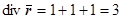 ,
, 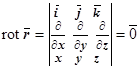 , то для центрального поля
, то для центрального поля 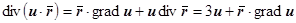 ,
, 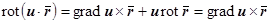 .
.
Векторное поле называется центрально-симметричным, если оно центрально, и функция u (M) зависит только от расстояния r, т.е. от длины радиуса-вектора точки М: 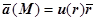 (
(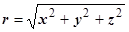 ). Так как
). Так как 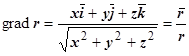 ,
, 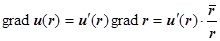 , то для центрально-симметричного поля
, то для центрально-симметричного поля 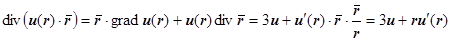 ,
, 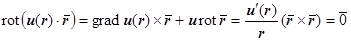 .
.
Найдем вид центрально-симметричного поля, для которого дивергенция равна нулю (в дальнейшем мы будем называть такие поля соленоидальными): 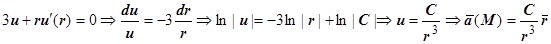 .
.
Таким образом, соленоидальны только те центрально-симметричные поля, в которых зависимость от r такая же, как в законах Кулона и всемирного тяготения. В связи с этим встают мировоззренческие вопросы о том, вычислял ли Господь Бог дивергенцию, когда создавал Вселенную, и о связи показателя степени в знаменателях законов Кулона и всемирного тяготения с пространственной размерностью мира, в котором мы живём
17.2.4. Векторные линии. Так как вектор 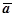 (M) определяется длиной и направлением в пространстве, задание в области V поля
(M) определяется длиной и направлением в пространстве, задание в области V поля 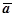 (M) равносильно заданию в V полей длин и направлений. Геометрической характеристикой, определяющей в V поле направлений, служит совокупность векторных линий.
(M) равносильно заданию в V полей длин и направлений. Геометрической характеристикой, определяющей в V поле направлений, служит совокупность векторных линий.
Определение. Векторной линией поля 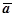 (M) называется любая линия, которая в каждой своей точке М касается вектора
(M) называется любая линия, которая в каждой своей точке М касается вектора 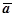 (M).
(M).
В силовой интерпретации поля векторными линиями являются силовые линии поля, в гидродинамической - векторные линии есть траектории, по которым движутся частицы жидкости (линии тока).
Получим дифференциальные уравнения векторных линий в декартовой системе координат. Пусть векторная линия определяется векторным уравнением 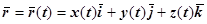 . Тогда касательный вектор к этой линии
. Тогда касательный вектор к этой линии 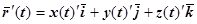 в любой точке должен быть коллинеарен полю, т.е.
в любой точке должен быть коллинеарен полю, т.е. 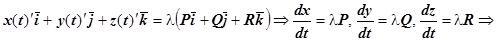
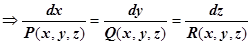 .
.
Эта записанная в симметричной форме система из трёх уравнений первого порядка и определяет векторные линии. Так как функции P, Q, R одновременно не обращаются в нуль, то в любой точке одна из них отлична от нуля. Пусть, например, в точке 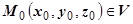
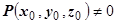 . Тогда систему можно записать в виде
. Тогда систему можно записать в виде 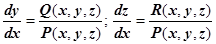 . Функции P, Q, R непрерывно дифференцируемы, поэтому для последней системы выполняются условия теоремы существования и единственности задачи Коши с начальными условиями
. Функции P, Q, R непрерывно дифференцируемы, поэтому для последней системы выполняются условия теоремы существования и единственности задачи Коши с начальными условиями 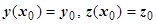 . Следовательно, через точку М 0 проходит, и при том единственная, интегральная кривая системы, которая и будет векторной линией поля.
. Следовательно, через точку М 0 проходит, и при том единственная, интегральная кривая системы, которая и будет векторной линией поля.
Пусть, например, поле 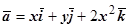 . Тогда векторные линии определяются системой
. Тогда векторные линии определяются системой 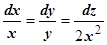 . Решая уравнение
. Решая уравнение 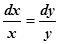 , получим
, получим 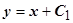 , из уравнения
, из уравнения 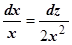 получаем
получаем 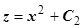 , таким образом, уравнения векторных линий
, таким образом, уравнения векторных линий 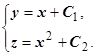
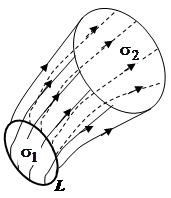 Пусть L - некоторая кривая в области V, не являющаяся векторной линией. Проведём через каждую точку L векторную линию; получившаяся в результате поверхность называется векторной поверхностью. Если L - замкнутая линия, то поверхность называется векторной трубкой. Основное свойство векторной трубки: векторная линия, вошедшая в трубку через поперечное сечение
Пусть L - некоторая кривая в области V, не являющаяся векторной линией. Проведём через каждую точку L векторную линию; получившаяся в результате поверхность называется векторной поверхностью. Если L - замкнутая линия, то поверхность называется векторной трубкой. Основное свойство векторной трубки: векторная линия, вошедшая в трубку через поперечное сечение 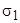 , может выйти из неё только через другое сечение
, может выйти из неё только через другое сечение 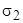 . Действительно, если бы векторная линия пересекла боковую поверхность векторной трубки, то через точку пересечения проходило бы две векторные линии, что, как мы установили, невозможно.
. Действительно, если бы векторная линия пересекла боковую поверхность векторной трубки, то через точку пересечения проходило бы две векторные линии, что, как мы установили, невозможно.
17.3.Поток векторного поля через поверхность.
В разделе 16.4. Поверхностные интегралы мы рассмотрели задачу о вычислении количества жидкости, протекающей через определённую сторону двусторонней поверхности 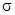 за единицу времени, и получили, что это количество выражается поверхностным интегралом
за единицу времени, и получили, что это количество выражается поверхностным интегралом 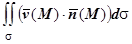 . Имеется целый ряд физических процессов, которые описываются аналогичными поверхностными интегралами, например, магнитная индукция.
. Имеется целый ряд физических процессов, которые описываются аналогичными поверхностными интегралами, например, магнитная индукция.
Среди других достоинств математики её мощь заключается, в частности, в способности исследовать процессы в самых разных областях естествознания, абстрагируясь от их физической сущности; приведённые выше примеры показывают естественность введения понятия потока векторного поля через поверхность.
17.3.1. Определение. Пусть 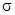 - двусторонняя гладкая поверхность, расположенная в области V, в которой задано поле
- двусторонняя гладкая поверхность, расположенная в области V, в которой задано поле 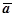 (M). Фиксируем выбором нормали
(M). Фиксируем выбором нормали 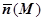 одну из двух сторон поверхности
одну из двух сторон поверхности 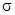 . Потоком векторного поля
. Потоком векторного поля 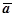 (M) через поверхность
(M) через поверхность 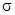 называется поверхностный интеграл первого рода по
называется поверхностный интеграл первого рода по 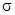 от скалярного произведения
от скалярного произведения 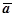 (M) на единичный вектор нормали
(M) на единичный вектор нормали 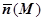 к выбранной стороне поверхности: П
к выбранной стороне поверхности: П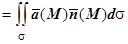 .
.
Существуют различные формы записи этого интеграла. Так как 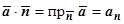 , поток может обозначаться П
, поток может обозначаться П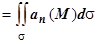 . Иногда произведение
. Иногда произведение 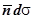 обозначают
обозначают 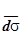 и называют этот вектор вектором элементарной площадки, тогда П
и называют этот вектор вектором элементарной площадки, тогда П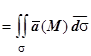 . Если связать
. Если связать 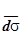 с проекциями
с проекциями 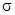 на координатные плоскости:
на координатные плоскости:
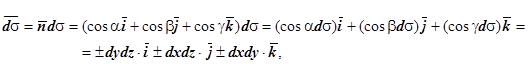
и использовать координатную запись поля 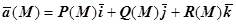 , то скалярное произведение в координатной форме даст П
, то скалярное произведение в координатной форме даст П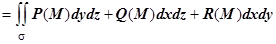 , т.е. поток может быть выражен и через поверхностный интеграл второго рода. Напомню, что в таком интеграле необходимо выбирать знак каждого слагаемого в зависимости от знака соответствующей координаты нормали.
, т.е. поток может быть выражен и через поверхностный интеграл второго рода. Напомню, что в таком интеграле необходимо выбирать знак каждого слагаемого в зависимости от знака соответствующей координаты нормали.
17.3.2. Свойства потока векторного поля. Согласно определению, поток - поверхностный интеграл, поэтому он имеет все свойства поверхностного интеграла. Понятно, что некоторые из этих свойств теряют смысл (интеграл от единичной функции, например), поэтому перечислим основные свойства потока.
1. Линейность. 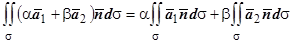 ;
;
2. Аддитивность. 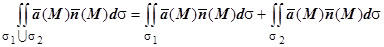 . Здесь
. Здесь 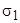 и
и 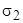 - кусочно-гладкие поверхности, которые могут пересекаться только по границам; нормали на этих поверхностях должны быть согласованы так, чтобы определять одну сторону всей составной поверхности
- кусочно-гладкие поверхности, которые могут пересекаться только по границам; нормали на этих поверхностях должны быть согласованы так, чтобы определять одну сторону всей составной поверхности 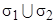 .
.
3. Поток меняет знак при изменении стороны поверхности (так как в каждой точке 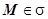 вектор
вектор 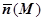 меняется на -
меняется на -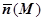 ).
).
17.3.3. Вычисление потока векторного поля. В соответствии с определением П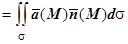
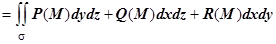 ,
,
поток может вычисляться и с помощью поверхностного интеграла первого рода, и с помощью поверхностного интеграла второго рода. В примере 2 раздела 16.4.4.3. Вычисление поверхностного интеграла второго рода было приведено вычисление потока поля 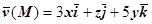 через часть плоскости
через часть плоскости 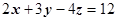 , ограниченную координатными плоскостями, в том и другом представлении. Рассмотрим более сложный пример.
, ограниченную координатными плоскостями, в том и другом представлении. Рассмотрим более сложный пример.
 Пример. Найти поток векторного поля
Пример. Найти поток векторного поля 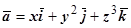 через полную внешнюю поверхность тела, ограниченного поверхностями
через полную внешнюю поверхность тела, ограниченного поверхностями 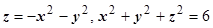 .
.
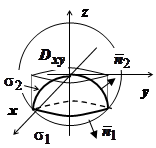
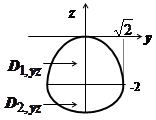
Решение. Поверхность состоит из двух частей: 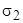 - часть поверхности параболоида
- часть поверхности параболоида 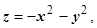 накрытая шапочкой
накрытая шапочкой 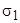 - частью нижней полусферы
- частью нижней полусферы 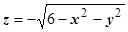 ; уровень пересечения этих поверхностей по оси Oz определяется уравнением
; уровень пересечения этих поверхностей по оси Oz определяется уравнением 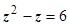 , откуда
, откуда 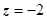 ; проекция линии пересечения на плоскость Oxy - окружность радиуса
; проекция линии пересечения на плоскость Oxy - окружность радиуса 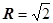 . Выпишем нормали:
. Выпишем нормали: 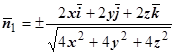 ; выбираем знак "+", так как на
; выбираем знак "+", так как на 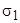 нормаль образует тупой угол с осью Oz, и коэффициент при
нормаль образует тупой угол с осью Oz, и коэффициент при 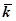 должен быть отрицателен (мы находимся в полупространстве
должен быть отрицателен (мы находимся в полупространстве 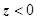 ). С учётом того, что на
). С учётом того, что на 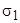
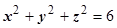 ,
, 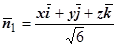 ,
, 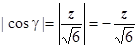 . Уравнение
. Уравнение 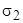 в виде поверхности уровня:
в виде поверхности уровня: 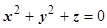 ,
, 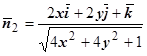 , знак "+", так как угол между
, знак "+", так как угол между 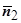 и осью Oz острый,
и осью Oz острый, 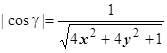 .
.
1. Вычисление с помощью поверхностного интеграла первого рода: П=П1+П2, П1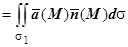 , П2
, П2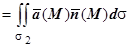 , обе поверхности однозначно проектируются на плоскость Oxy в круг радиуса
, обе поверхности однозначно проектируются на плоскость Oxy в круг радиуса 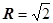 , поэтому П1
, поэтому П1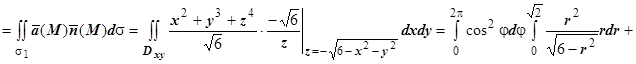
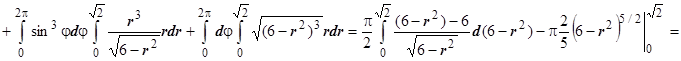
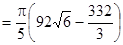 .
.
П2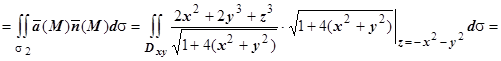
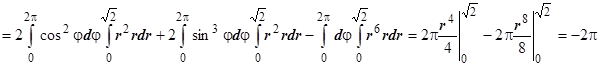 .
.
П=П1+П2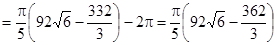 .
.
 2. Посмотрим, к каким вычислениям приводит применение поверхностного интеграла второго рода.
2. Посмотрим, к каким вычислениям приводит применение поверхностного интеграла второго рода. 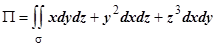 . Для вычисления
. Для вычисления 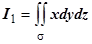 придется разбить полную поверхность
придется разбить полную поверхность 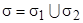 на части
на части 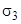 , находящуюся в полупространстве
, находящуюся в полупространстве 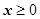 , где
, где 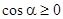 , и
, и 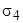 , находящуюся в полупространстве
, находящуюся в полупространстве 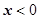 , где
, где 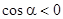 ;
; 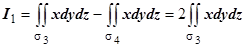 (с учётом того, что подынтегральная функция меняет знак при переходе от
(с учётом того, что подынтегральная функция меняет знак при переходе от 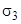 к
к 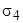 )
) 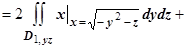
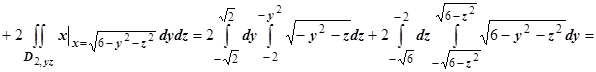
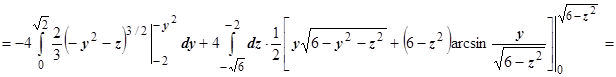
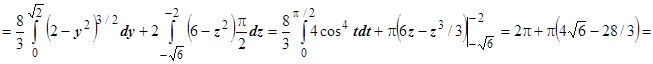
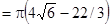 .
.
Интеграл 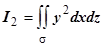 равен нулю, так как подынтегральная функция чётна по у, а интегралы по частям поверхности, находящихся в полупространствах
равен нулю, так как подынтегральная функция чётна по у, а интегралы по частям поверхности, находящихся в полупространствах 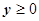 , где
, где 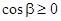 , и
, и 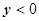 , где
, где 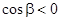 , берутся с разными знаками.
, берутся с разными знаками.
Интеграл 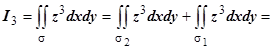 (в соответствии со знаками
(в соответствии со знаками 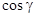 на
на 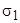 и
и 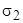 )
) 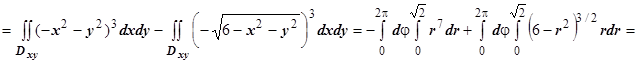
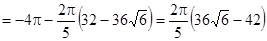 . Поток
. Поток 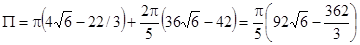 .
.
Ответы, как и должно быть, совпали, однако вычисления с помощью криволинейного интеграла первого рода оказались существенно более простыми.
17.3.4. Теорема Остроградского. Пусть 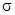 - кусочно-гладкая замкнутая поверхность, ограничивающая область V,
- кусочно-гладкая замкнутая поверхность, ограничивающая область V, 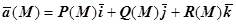 - гладкое векторное поле. Тогда поток поля
- гладкое векторное поле. Тогда поток поля 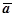 через внешнюю сторону
через внешнюю сторону 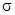 равен тройному интегралу от дивергенции поля
равен тройному интегралу от дивергенции поля 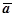 по V:
по V:
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 625; Нарушение авторских прав?; Мы поможем в написании вашей работы!