
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Нагрузка от сил инерции жидкости
|
|
|
|
Найдем теперь удельное давление вращающейся жидкости на обечайку ротора.
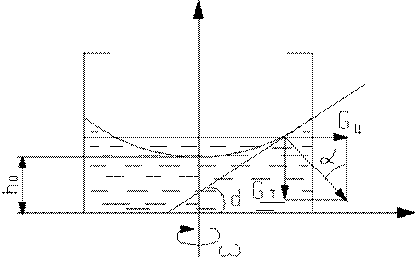 Рисунок 19 - Форма свободной поверхности жидкости во вращающемся цилиндре
Рисунок 19 - Форма свободной поверхности жидкости во вращающемся цилиндре
| Рассмотрим прямой круговой цилиндр, закрытый снизу днищем, а сверху- кольцевой крышкой и вращающийся с угловой скоростью w вокруг своей вертикальной оси. Ввиду симметрии системы ограничимся рассмотрением осевого сечения цилиндра с системой координат x, y (рисунок 19). |
Предполагаем, что жидкость вращается вместе с цилиндром, не перемещаясь относительно его стенок. На элементарную массу dm на свободной поверхности вращающейся жидкости действует центробежная сила 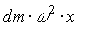 и сила тяжести
и сила тяжести 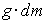 , результирующая которых должна быть перпендикулярна поверхности, являющейся поверхностью уровня. Если касательная к сечению поверхности, то:
, результирующая которых должна быть перпендикулярна поверхности, являющейся поверхностью уровня. Если касательная к сечению поверхности, то:
 , (58)
, (58)
Интегрируя находим уравнение сечения свободной поверхности поверхностью xy:
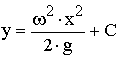 , (59)
, (59)
Полученное выражение- уравнение параболы, отнесенной к осевой оси. Следовательно, свободная поверхность жидкости- параболоид вращения.
При 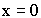 , имеем
, имеем 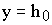 , следовательно
, следовательно 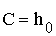 и:
и:
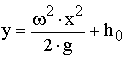 , (60)
, (60)
При 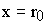 имеем
имеем 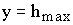 и
и
 , (61)
, (61)
Из уравнения (), положив 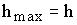 находим, что скорость, при которой жидкость поднимается на высоту h, равна:
находим, что скорость, при которой жидкость поднимается на высоту h, равна:
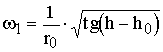 , (62)
, (62)
Положим теперь, что скорость вращения 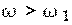 . Жидкость будет стремиться подняться на высоту . Жидкость будет стремиться подняться на высоту 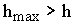 и при отсутствии крышки начнет переливаться через край. Так как крышка этого не допускает, жидкость начнет скапливаться под крышкой и покроет ее по кольцу с внутренним радиусом r (рисунок 20).
Рассуждая совершенно так же, как в случае открытого цилиндра, мы приходим к выводу, что уравнение () остается в том же виде, другим будет лишь значение постоянной С, которое мы найдем, положив в уравнение () и при отсутствии крышки начнет переливаться через край. Так как крышка этого не допускает, жидкость начнет скапливаться под крышкой и покроет ее по кольцу с внутренним радиусом r (рисунок 20).
Рассуждая совершенно так же, как в случае открытого цилиндра, мы приходим к выводу, что уравнение () остается в том же виде, другим будет лишь значение постоянной С, которое мы найдем, положив в уравнение () 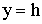 при при 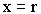
| 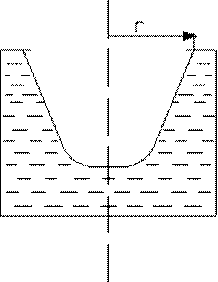 Рисунок 20 - Форма свободной поверхности жидкости во вращающемся цилиндре с крышкой
Рисунок 20 - Форма свободной поверхности жидкости во вращающемся цилиндре с крышкой
|
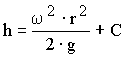
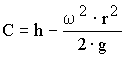 , (63)
, (63)
Подставляя значение С в уравнение (63), получим:
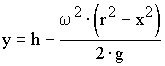 , (64)
, (64)
Из уравнения (3.85) имеем:
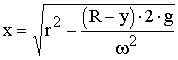 , (65)
, (65)
При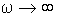 получаем:
получаем:
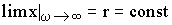 , (66)
, (66)
т.е. при достаточно больших скоростях вращения ротора (соответствующих рабочим условиям) свободная поверхность жидкости может считаться цилиндрической. Установив форму свободной поверхности во вращающемся цилиндре, найдем теперь давление ее на обечайку.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 573; Нарушение авторских прав?; Мы поможем в написании вашей работы!