Векторы в координатной форме

Равное его длине, умноженной на косинус угла между вектором и осью.

В

А С

О А₀ А₁ В₁ W

0 1 w₁ w₂

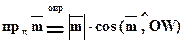
Свойства

5.5.1.

Число назовем координатой вектора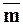по оси OW.

Следовательно, проекция вектора на числовую ось (или его компонента)

численно равна координате вектора по этой оси:

.

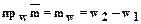5.5.2. .

5.5.3. .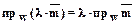

5.5.4. .

6.1. Составляющая вектора по числовой оси

Составляющей вектора по числовой оси OW будем называть

вектор, соединяющий проекции его начала и конца на данную ось.

6.1.1. Составляющую вектора по числовой оси можно найти с помощью

орта этой оси:

6.1.1.1. В прямоугольной декартовой системе координат орты координатных осей обозначают так: 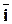- орт оси OX, 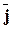- орт оси OY, 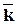- орт оси OZ.

Орты задают направление и масштаб числовых осей.

6.1.1.2. Углы между любым вектором 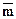и осями координат (или ортамикоординатных осей) обозначают так: .

6.1.1.3. Направляющими косинусами вектора 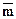будем назвать косинусы угловмежду этим вектором и осями координат: .

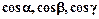6.1.2. В прямоугольной декартовой системе координат составляющие

любого вектора 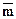можно найти по формулам:

- составляющая вектора 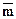по оси абсцисс ;

- составляющая вектора 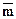по оси ординат ;

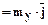- составляющая вектора 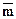по оси аппликат .

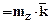6.2. Разложение вектора на составляющие по координатным осям

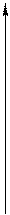Z

z₂ B₃

В

z₁ A₃

A

O A₂ B₂

y₁ y₂ Y

х₁ А₁ А₀

х₂ В₀

Х

6.2.1. Любой вектор равен сумме всех своих составляющих по осям координат.

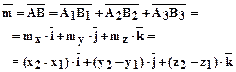
- разложение вектора на составляющие по координатным осям.

6.2.2. Для того, чтобы задать вектор, достаточно задать все его координаты.

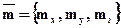- задание вектора в координатной форме;

тогда 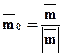- вектор единичной длины сонаправленный с , т.е. - задание единичного вектора в координатной форме.

6.2.3. Действия с векторами в координатной форме

Пусть векторы заданы своими координатами:

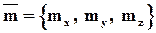;; ;  - скаляр.

6.2.3.1.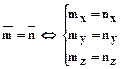

6.2.3.2.

6.2.3.3.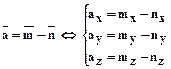

6.2.3.4.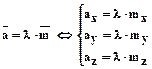

6.2.3.5.

6.2.3.6.

6.2.3.7. .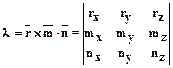

6.2.3.8. .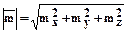

6.2.3.9. .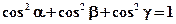

Дата добавления: 2014-01-07