Лекция 4. 22.02.13

Вставка 994

Коэффициенты двухфакторной модели.

Интерпретация коэффициентов регрессии. Коэффициенты регрессии бетта 2 и бетта 3 указывают на изменение результирующего признака у при изменение соответствующего факторного признака х1 и х2 на единицу.

Для сравнения степени влияния факторных признаков на результирующий признак используют средний частный коэффициенты эластичности.

эти коэффициенты показывают на сколько процентов в среднем изменится результирующий признак при измени факторного признака на 1%.

МНОЖЕСТВЕННЫЙ КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ.

Корреляционная связь может существовать как между двумя факторами (интеркорреляция) так и между несколькими факторами (мультикоминеарностью). Существование корреляционной связи может быть выявлено с помощью матрицы парного коэффициентов корреляции.

вставка

Наличие мультиколениарности можно подтвердить найдя опредилитель матрицы парных коэффициентов корреляции.

Если связь между факторами полностью отсутствуют, то недиагональные элементы матрицы будут равны 0, тогда определитель матрицы будет равен 1.

Если же связь между факторами будет очень тесной то определитель будет близок к 0.

Коэффициент множественной корреляции определяется через матрицы парных коэффициентов корреляции.

Вставка

Дельта

Коэффициент множественной корреляции. В частном случае когда число факторов равно 2. Y=f(x1,x2) определяется по следующей формуле.

Вставка.

Причём множественный коэффициент корреляции всегда больше или равен максимальному парному коэффициенту корреляции.

Качество построенной модели в целом оценивают коэффициентом множественной детерминации. R2.

Статистическую значимость уравнения множественной регрессии оценивают по f критерию Фишера-Снедекора.

Вставка

R2 – множественный коэффициент детерминации.

N – число наблюдений

M – число факторов в уравнении.

Интерпретация модели регрессии

Полученная модель позволяет сформулировать некоторые количественные выводы если воспользоваться следующими понятиями.

Эмпирический коэффициент детерминации – вставка. Этот коэффициент показывает долю вариаций результирующего признака у, обусловленную вариацией факторного признака х.

0≤R2≤1

Эмпирическое корреляционное отношение корень из формулы выше.

Вставка.

Пример.

Рассчитаем коэффициент детерминации r2 корреляционное отношение r и средний коэффициент эластичности на примере о 10 предприятиях.

Предварительно рассчитаем вставка

Вставка центр р2.

Вывод: таким образом 85,6% вариаций объясняется включением в модель факторного признака, но остальные 14,4% объясняются прочими неучтенными моделями признаками.

Оценим корреляционное отношение. Вставка.

РЯДЫ ДИНАМИКИ.

Динамикой называют процесс развития явления во времени. Ряд динамики – это изменение во времени какого-либо показателя, отражающее развитие экономического явления. Элементами рядов динамики являются: уровни(у) и моменты времени (t).

Ряды динамики позволяют характеризовать развития изучаемого явления во времени.

Изучать динамику явления при помощи системы статистических показателей.

Выявлять и моделировать основную тенденцию развития изучаемого явления.

Аппроксимировать данные и прогнозировать изучаемый показатель методом экстраполяции.

Изучать и учитывать при прогнозировании периодические (сезонные) колебания показателей.

Все ряды динамики делятся на стационарные и нестационарные. Если характеристики изучаемого процесса постоянны и не зависят от времени то процесс и соответствующий ряд динамики считаются стационарным.

Вставка

Экономические процессы как правило не являются стационарными так как содержат тенденцию развития.

Математически их можно преобразовать в стационарные ряды путем выделения тенденции.

Yt= f(T)+e

Где Т – тренд ряда, те математическая функция, характеризующая закономерность развития явления во времени.

При изучение динамики явления за продолжительный период, уровни ряда могут обнаруживать регулярные колебания повторяющиеся через равные промежутки времени. Такие колебания называются периодическими.

Если период колебания несколько лет, то такие колебания называются циклическими.

Длина цикла зависит от вида экономической деятельности и охватывает обычно от 3 до 12 лет.

Регулярные колебания называются сезонными когда цикл колебания примерно равен году.

Ряд с тенденцией и периодическими колебаниями.

В общем случае в рядах динамики изучаемого явления можно обнаружить следующие компоненты

Т – основная тенденция тренд.

S – сезонная волна

К – циклическая конъюнктурная составляющая.

Е – случайные колебания или помехи

Для описаний временного ряда применяется аддитивная и мультипликативная модель

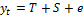
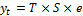
Тренд характеризует основную тенденцию развития а все остальные перманенты затрудняют процедуру его определения.

задача Нахождения кривой которая сгладила сезонные и конъюнктурные колебания.

Дата добавления: 2014-01-06