Сдвиг элементов конструкции

В основе любых геометрических изменении элемента детали под нагрузкой лежат линейные и угловые деформации.

Характеристикой угловых деформации является абсолютный сдвиг S, мм и относительный сдвиг γ, ◦.

Выделим элемент детали, которая испытывает сдвиг.

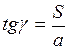
abcd – повернуть.

А – площадь поперечного сечения, abcd напряжения по плоскому поперечному сечению.

Предположим, касательная приложена равномерно.

Призматический элемент abcd. Находится в состоянии чистого сдвига, т.е. на гранях касательного движения.

Правило парности состояния.

- формула выражения Гука при сдвиге.

Где G – модуль упругости I рода, или модуль сдвига.

При сдвиге рис (*) следовательно возникает плоское напряженное состояние и чистый сдвиг эквивалентен растяжению и сжатию элемента в диагональных направлениях.

1. Кручение элементов конструкций. Условие прочности и условие жесткости при кручении.

Кручение – такой вид деформации, при котором в поперечных сечениях внутренние усилия проводятся только к крутящему моменту. Такое кручение называют свободным или чистым.

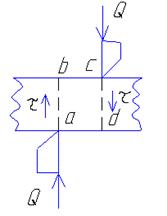
Крутящий момент Т и τ лежат на поперечном сечении. Обычно в кручении принимается гипотеза плоских сечений. Сечения стержня до и после нагружения остаются плоскими, т.е. радиусы остаются прямолинейными. Если волной, то пойдет депланация. Принимаем гипотезу прямолинейноси до и после нагружения.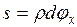

в виду малости углов и γ

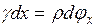и (*).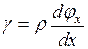

Согласно закону Гука, тогда из (*) получаем, что

,(**)

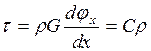где С- крутильная жесткость стержня.

Для стержня постоянного сечения С постоянного значения.

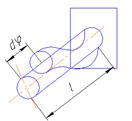
Касательное напряжение τ изменяется по линейному закону, прямо пропорционально текущему радиусу ρ. Если принять элементарную площадку dA в виде тонкого кольца толщиной dρ, то связь между τ и Т

Подставляем в (**)

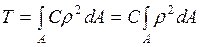
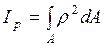
Используя (**) и исходя что:

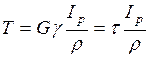
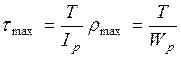
- момент сопротивления.

Условие стержня (круглого сечения) при кручении определяется

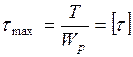
Перемещения определяется из следующего соотношения в общем виде

или ; .

- жесткость при кручении; ЕА- при сжатии; ЕI – при изгибе.

При постоянных значениях, т.е. T=const

Условие жесткости при кручении.

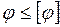
- допустимый.

- относительный.

Напряженное состояние при чистом кручении.

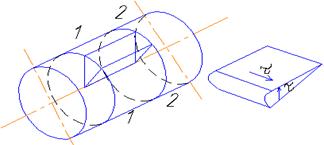Элемент при кручении выделен двумя сечениями, перпендикулярные оси 1-1, 2-2. а также двумя радиальными сечениями. Находится в состоянии чистого сдвига.

Проверка на прочность

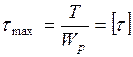
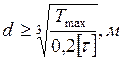
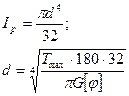
Дата добавления: 2014-01-07