
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 2. Глава 1. Анализ рычажных механизмов
|
|
|
|
Глава 1. Анализ рычажных механизмов.
В данной главе будут рассмотрены вопросы:
1. структурный анализ механизма (изучение строения механизма);
2. изучение классов и видов кинематических пар.
3. определение числа степеней свободы механизма и определение наличия или отсутствия избыточных связей; в случае наличия – дать рекомендации по способу их устранения;
4. кинематический анализ механизма.
§1.1
Примечание:
Кинематическая пара существует, если не происходит деформации звеньев, образующих эту пару, и не должно происходить отрыва звеньев одно от другого, образующих кинематическую пару.
Примечание:
Ограничения, накладываемые на независимые движения звеньев, образующих кинематическую пару, называются – условия связи S.
Число степеней свободы механизма
W=S+H,
где Н – подвижность.
Любое незакрепленное тело в пространстве имеет 6 степеней свободы, на плоскости – 3.
Классификация кинематических пар проводят либо по числу связей, либо по числу подвижностей:
Число связей Класс КП Число подвижностей
S=1 P I H=5
S=2 P II H=4
S=3 P III H=3
S=4 P IV H=2
S=5 P V H=1
Существует 5 классов кинематических пар.
Примеры различных КП смотри рис. 4-95.
Кинематические пары по характеру контакта звеньев, образующих КП, разделяют на:
1. низшие:
· вращательные;
· поступательные;
2. высшие.
Контакт звеньев в низшей КП осуществляется по поверхности. Контакт звеньев в высшей КП – либо по линии, либо в точке.
§1.2 Определение числа степеней свободы рычажных механизмов.
1.2.1 Плоские механизмы.
В плоском механизме все звенья движутся в одной плоскости, все оси параллельны друг другу и перпендикулярны плоскости механизма.
ФОРМУЛА ЧЕБЫШЕВА: W пп =3n -2p н -p в ,
Где n – число подвижных звеньев механизма, рн – число низших КП, рв – число высших КП.
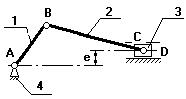
n=3
pн=4
рв=0
W=3.3-2.2=1
Рис.1.2.1
1.2.2 Пространственные механизмы.
В пространственном механизме оси непараллельны, звенья могут двигаться в разных плоскостях.
Wпр= 6n - (S1+ S2+ S3+ S4+ S5)
Допустим, что механизм, изображенный на рис.1.2.1 – пространственный и все кинематические пары 5-го класса, т.е. одноподвижны AV,BV,CV,DV, тогда
Wпр= 6n - (5pV+4pIV+3pIII+2pII+pI)
Wпр= 6.3 - 5.4 = -2 à статически неопределимая ферма.
Для получения Wдейств=0, необходимо добавить 3 движения.
q= Wдейств - Wпр = 1 - (-2) = 3,
где q – избыточные связи.
Для того чтобы их устранить, надо изменить класс некоторых кинематических пар, при этом нельзя изменять класс КП А. Поэтому, сделаем КП В – сферическим шарниром, т.е. 3-го класса (добавим 2 подвижности), а КП С – 4-го класса (добавим 1 подвижность). Тогда
Wпр= 6.3 - (5.2 + 4.1 + 3.1) = 18 - 17 = 1
n
ФОРМУЛА СОМОВА-МАЛЫШЕВА: Wпр= 6.n - ΣSi + q
i=1
§1.3 Кинематический анализ рычажных механизмов.
1.3.1 Основные понятия и определения.
Зависимость линейных координат в какой-либо точке механизма от обобщенной координаты – линейная функция положения данной точки в проекциях на соответствующие оси координат.
Хс= f(j1)
Зависимость угловой координаты какого-либо звена механизма от обобщенной координаты – угловая функция положения данного звена.
j2= f(j1)
Первая производная линейной функции положения точки по обобщенной координате – линейная передаточная функция данной точки в проекциях на соответствующие оси координат (иногда называют «аналог линейной скорости…»)

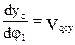

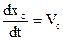

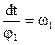



полная скорость т. С будет 
Первая производная угловой функции положения звена по обобщенной координате – передаточное отношение.

Вторая производная линейной функции положения по обобщенной координате – аналог линейного ускорения точки в проекциях на соответствующие оси.


Вторая производная угловой функции положения звена по обобщенной координате – аналог углового ускорения звена.
1.3.2 Аналитический способ определения кинематических параметров рычажных механизмов.
Дано: w1, lAB, lBS2, lBC, lAC
Определить: vi, ai, w2, e2.
Для исследования плоских рычажных механизмов для решения данной задачи целесообразно использовать метод проецирования векторного контура на оси координат.
Для определения функции положения точки С представим длины звеньев в виде векторов.
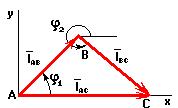 Условие замкнутости данного контура:
Условие замкнутости данного контура:
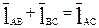 (1)
(1)
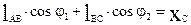 (2)
(2)

 (3)
(3)
рис.1.3.2 из (3) следует, что
 (4)
(4)
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 319; Нарушение авторских прав?; Мы поможем в написании вашей работы!