ЛЕКЦИЯ 9. Общая нормаль, проведенная в точке контакта сопряженных поверхностей, проходит через линию центров О1О2 и делит эту линию на части

Общая нормаль, проведенная в точке контакта сопряженных поверхностей, проходит через линию центров О1О2 и делит эту линию на части, обратно пропорциональные отношению угловых скоростей.

ЛЕКЦИЯ 8.

Сопряженные поверхности – поверхности, которые постоянно или с определенной периодичностью входят в зацепление друг с другом.

По отношению к начальным окружностям сопряженные поверхности могут занимать различные положения. Правильным положением является то, которое удовлетворяет основной теореме зацепления, теореме о мгновенном передаточном отношении, которое формулируется:

Передаточное отношение

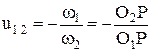(см рис. 4.4.1)

Сопряженные профили должны удовлетворять следующим требованиям:

1. быть простыми в изготовлении (технологичными);

2. иметь высокий КПД.

Таким требованиям удовлетворят эвольвентные профили.

§4.3 Эвольвента и ее свойства.

Эвольвента образуется путем перекатывания производящей прямой K_yN_y без скольжения по основной окружности радиуса r_b.

Радиус произвольной окружности – r_y. ON_y || tt

Из треугольника ON_yK_y следует, что

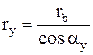(1)

Т.к. K_yN_y перекатывается без скольжения по основной окружности, то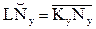

r_b(q_y + a_y) = r_b ^. tg a_y

q_y = tg a_y - a_y (2)

q_y = inv a_y

q_y – инволюта;

Уравнения (1) И (2) являются уравнениями эвольвенты в параметрической форме.

a_у – угол профиля эвольвенты для точки К_у, лежащей на произвольной окружности.

a – угол профиля эвольвенты для точки К, лежащей на делительной окружности радиуса r.

Угол профиля эвольвенты для точки К_b, лежащей на основной окружности, равен нулю: a_b=0.

Свойства эвольвенты.

1. Форма эвольвенты зависит от радиуса основной окружности. При стремлении r_b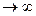,эвольвента превращается в прямую линию (пример рейка).

2. Производящая прямая K_yN_y является нормалью к эвольвенте в данной тоске.

3. Эвольвента начинается от основной окружности. Внутри основной окружности точек эвольвенты нет.

§4.4 Элементы эвольвентного зубчатого колеса.

Делительной окружностью называется окружность стандартных шага р, модуля m и угла профиля a.

Шаг – расстояние между одноименными точками двух соседних профилей зубьев, измеренные по дуге соответствующей окружности.

Модулем называется часть диаметра делительной окружности, приходящаяся на один зуб.

Модуль m,[мм] – стандартная величина и определяется по справочникам, исходя из трех рядов:

1 ряд – наиболее предпочтительный;

2 ряд – средней предпочтительности;

3 ряд – наименее предпочтительный.

Модуль характеризует высоту зуба. Чем больше зуб, тем более шумной становится зубчатая передача.

Угол профиля – угол между касательной к эвольвенте в данной точке и радиус-вектором данной точки (см. чертеж эвольвенты).

Угол профиля для точки, лежащей на делительной окружности, является величиной стандартной и равной 20 ^о (хотя лучше 25 ^о).

4.4.1 Основные расчетные зависимости для определения параметров эвольвентного зубчатого колеса.

Из (1) следует, что радиус делительной окружности

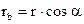(3)

модуль по ГОСТу определяется

m = p / p p = p ^. m (4)

2p ^. r = p ^. z

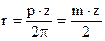(5)

2p ^. r_y = p_y ^. z

à

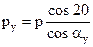(6)

по основной окружности

a_y = 0 à p_b = p cos 20^o (7)

4.4.2 Виды зубчатых колес.

p = s + e (8)

s = + Δ^. m (9)

где Δ – коэффициент изменения толщины зуба.

В зависимости от знака коэффициента Δ различают виды зубчатых колес:

1. Δ = 0 s = e = p/2 нулевое зубчатое колесо;

2. Δ > 0 s > e положительное зубчатое колесо;

3. Δ < 0 s < e отрицательное зубчатое колесо.

§4.5 Эвольвентная зубчатая передача и ее свойства (рис. 11-86).

Эвольвентную зубчатую передачу составляют, как минимум, из 2-х зубчатых колес, при этом в рассмотрение вводится две начальные окружности радиусами r_w1 и r_w2.

Меньшее зубчатое колесо в обычной понижающей зубчатой передаче называется шестерня.

Вместо производящей прямой здесь вводится в рассмотрение линия зацепления N₁N₂, которая одновременно касается 2-х основных окружностей r_b1 и r_b2.

Линия зацепления является геометрическим местом точек контакта сопряженных эвольвентных профилей. В точке В₁ пара эвольвент, которые в данный момент времени контактируют в точке К, входят в зацепление. В точке В₂ этаже пара эвольвент из зацепления выходят.

На линии зацепления N₁N₂ все взаимодействующие эвольвенты при зацеплении касаются друг друга. Вне участка N₁N₂ эвольвенты пересекаются, и если такое случится, то произойдет заклинивание зубчатого колеса.

Угол N₁O₁P = N₂J₂P = a_w – угол зацепления.

Для передачи, составленной из нулевых зубчатых колес a_w=20 ^o

Для передачи, составленной из положительных з. к. a_w>20 ^o

Для передачи, составленной из отрицательных з. к. a_w<20 ^o

c=c*^.m - радиальный зазор, величина стандартная, необходим для нормального обеспечения смазки.

c* - коэффициент радиального зазора, по ГОСТ c*=0.25 (c*=0.35).

Между делительными окружностями у^.m – это воспринимаемое смещение.

у – коэффициент воспринимаемого смещения, он имеет знак, и в зависимости от знака различают:

1. у=0 у ^. m=0 – нулевая зубчатая передача;

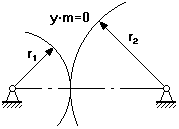
2. у>0 у ^. m>0 – положительная зубчатая передача;

3. у<0 у ^. m<0 – отрицательная зубчатая передача;

Свойства эвольвентного зацепления.

1. Эвольвентное зацепление молочувствительно к погрешностям изготовления, т.е. при отклонении межосевого расстояния от номинала передаточное отношение зубчатой передачи не изменится.

2. Линия зацепления N₁N₂ является общей нормалью к сопряженным эвольвентным профилям.

3. Контакт эвольвент осуществляется только на линии зацепления.

4.5.1 Основные расчетные зависимости для определения основных параметров эвольвентных зубчатых передач.

1. Определение угла зацепления.

inv a_w = inv a + 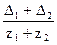(1)

где Δ_1, Δ₂ – изменение толщины зуба;

z₁, z₂ – число зубьев.

2. Определение межосевого расстояния зубчатых передач.

а_w = r_w1 + r_w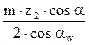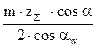2 =+= += (2)

z_Σ = z₁ + z₂

3. Определение коэффициента воспринимаемого смещения y.

а_w = r₁ + r₂ + y m

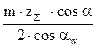=++ y m

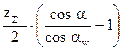y = (3)

4.5.2 Качественные показатели зубчатых передач.

к ним относятся:

Дата добавления: 2014-01-07