Урсул А.Д. Проблема информации в современной науке. Философские очерки. - М.: Наука, 1975

2. Кількість інформації. Одиниця інформації. Поняття ентропії. Можливості та обмеження класичних кількісних підходів до поняття інформації. (2 год.)

ПОНЯТИЕ КОЛИЧЕСТВА ИНФОРМАЦИИ

Предположим, что какое-то событие имеет m равновероятных исходов. Таким событием может быть, например, появление любого символа из алфавита, содержащего m таких символов. Как измерить количество информации, которое может быть передано при помощи такого алфавита? Это можно сделать, определив число N возможных сообщений, которые могут быть переданы при помощи этого алфавита. Если сообщение формируется из одного символа, то N = m, если из двух, то N = m*m = m². Если сообщение содержит n символов (n - длина сообщения), то N = mⁿ. Казалось бы, искомая мера количества информации найдена. Ее можно понимать как меру неопределенности опыта, если под опытом подразумевать случайный выбор какого-либо сообщения из некоторого числа возможных. Однако эта мера не совсем удобна. При наличии алфавита, состоящего из одного символа, т.е. когда m = 1, возможно появление только этого символа. Следовательно, неопределенности в этом случае не существует, и появление этого символа не несет никакой информации. Между тем, значение N при m = 1 не обращается в нуль. Для двух независимых источников сообщений (или алфавита) с N₁ и N₂ числом возможных сообщений общее число возможных сообщений N = N₁N₂, в то время как логичнее было бы считать, что количество информации, получаемое от двух независимых источников, должно быть не произведением, а суммой составляющих величин.

Выход из положения был найден Р.Хартли, который предложил информацию I, приходящуюся на одно сообщение, определять логарифмом общего числа возможных сообщений N:

I(N)=log N (1)

Если же все множество возможных сообщений состоит из одного (N = m = 1), то I(N) = log 1 = 0, что соответствует отсутствию информации в этом случае. При наличии независимых источников информации с N₁ и N₂ числом возможных сообщений

I(N) = logN = log N₁N₂ = log N₁ + logN₂,

т.е. количество информации, приходящееся на одно сообщение, равно сумме количеств информации, которые были бы получены от двух независимых источников, взятых порознь. Формула, предложенная Хартли, удовлетворяет предложенным требованиям. Поэтому ее можно использовать для измерения количества информации.

Если возможность появления любого символа алфавита равновероятна (а мы до сих пор предполагали, что это именно так), то эта вероятность p = 1/m. Полагая, что N=m,

I = logN = log m = log1/p = -log p, (2)

т.е. количество информации на каждый равновероятный сигнал равно минус логарифму вероятности отдельного сигнала.

Полученная формула позволяет для некоторых случаев определить количество информации. Однако для практических целей необходимо задаться единицей его измерения. Для этого предположим, что информация - это устраненная неопределенность. Тогда в простейшем случае неопределенности выбор будет производиться между двумя взаимоисключающими друг друга равновероятными сообщениями, например между двумя качественными признаками: положительным и отрицательным импульсами, импульсом и паузой и т.п. Количество информации, переданное в этом простейшем случае, наиболее удобно принять за единицу количества информации. Именно такое количество информации может быть получено, если применить формулу (2) и взять логарифм по основанию 2. Тогда

I = -log₂p = -log₂1/2 = log₂2 = 1

Полученная единица количества информации, представляющая собой выбор из двух равновероятных событий, получила название двоичной единицы, или бита. Название bit образовано из двух начальных и последней букв английского выражения binary digit, что значит двоичная единица. Бит является не только единицей количества информации, но и единицей измерения степени неопределенности. При этом имеется в виду неопределенность, которая содержится в одном опыте, имеющем два равновероятных исхода.

На количество информации, получаемой из сообщения, влияет фактор неожиданности его для получения того или иного сообщения. Чем меньше эта вероятность, тем сообщение более неожиданно и, следовательно, более информативно. Сообщение, вероятность которого высока и, соответственно, низка степень неожиданности, несет немного информации.

Р. Хартли понимал, что сообщения имеют различную вероятность и, следовательно, неожиданность их появления для получателя неодинакова. Но, определяя количество информации, он пытался полностью исключить фактор "неожиданности". Поэтому формула Хартли позволяет определить количество информации в сообщении только для случая, когда появление символов равновероятно и они статистически независимы. На практике эти условия выполняются редко. При определении количества информации необходимо учитывать не только количество разнообразных сообщений, которые можно получить от источника, но и вероятность их получения.

Наиболее широкое распространение при определении среднего количества информации, которое содержится в сообщениях от источников самой разной природы, получил подход К. Шеннона. Рассмотрим следующую ситуацию.

Источник передает элементарные сигналы k различных типов. Проследим за достаточно длинным отрезком сообщения. Пусть в нем имеется N₁ сигналов первого типа, N₂ сигналов второго типа,..., N_k сигналов k -го типа, причем N₁ + N₂ +... + N_k = N - общее число сигналов в наблюдаемом отрезке, f₁, f₂,..., f_k - частоты соответствующих сигналов.

При возрастании длины отрезка сообщения каждая из частот стремится к фиксированному пределу, т.е.

lim f_i = p_i (i = 1,2,..., k), где p_i можно считать вероятностью сигнала. Предположим, получен сигнал i -того типа с вероятностью p_i, содержащий -logp_i единиц информации. В рассматриваемом отрезке i -й сигнал встретится примерно Np_i раз (будем считать, что N достаточно велико), и общая информация, доставленная сигналами этого типа, будет равна произведению -Np_ilogp_i. То же относится к сигналам любого другого типа, поэтому полное количество информации, доставленное отрезком из N сигналов, будет примерно равно

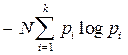
Чтобы определить среднее количество информации, приходящееся на один сигнал, т.е. удельную информативность источника, нужно это число разделить на N. При неограниченном росте числа сигналов приблизительное равенство перейдет в точное. В результате будет получено асимптотическое соотношение - формула Шеннона:

I =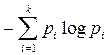

В последнее время она стала не менее распространенной, чем знаменитая формула Эйнштейна E = mc². Оказалось, что формула, предложенная Хартли, представляет собой частный случай более общей формулы Шеннона. Если в формуле Шеннона принять, что

p_1. = p₂ =... = p_i =... p_N = 1/N,

то

I = = =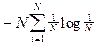

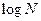
Знак минус в формуле Шеннона не означает, что количество информации в сообщении - отрицательная величина. Объясняется это тем, что вероятность p, согласно определению, меньше единицы, но больше нуля. Так как логарифм числа, меньшего единицы, т.е. logp_i - величина отрицательная, то произведение вероятности на логарифм числа будет положительным.

3. Семантична концепція інформації. Поняття тезаурусу. Закономірності сприяння інформації в рамках тезаурусної моделі. (2 год.)

Как известно, понятие энтропии, как и понятие количества информации, определяется в рамках классической статистической теории информации. Важнейшим исходным положением этой теории, как известно, является отвлечение от смысла сообщений, позволяющее рассматривать их как сигналы, для которых существенен только факт их появления или непоявления перед приемником. Введение объективной меры возможности этого факта - его вероятности - позволяет получить объективную характеристику информационной ситуации - энтропию. Естественное обобщение этой ситуации - замена сигнала любым случайным событием и замена приемника (его природа несущественна в данном случае) некоторым “объективным наблюдателем” превращает понятия количества информации и энтропии в чисто математические.

Действительно, в одном из определений энтропией H (X) дискретного ансамбля сообщений X называется математическое ожидание собственного количества информации сообщений ансамбля:

H (X) = E J (X) = å J (X) p (x) = - å p (x) log p (x),

Дата добавления: 2014-01-07