D – центрированной грани

Зональные погасания

Сериальные погасания

Эти погасания обусловлены присутствием винтовых осей. Особенностью в отношении погасаний обладают плоскости, перпендикулярные винтовым осям. Это связано с тем, что наличие винтовой оси n-го порядка приводит к изменению периода вдоль направлений, параллельных оси. То есть по сравнению с простой поворотной осью ВИНТОВАЯ ОСЬ приводит к появлению дополнительных узловых плоскостей перпендикулярных ей. Для таких плоскостей разность хода лучей будет содержать дробное число длин волн, и будет наблюдаться соответствующее погасание. Винтовые оси обычно располагаются вдоль координатных осей, поэтому закономерности погасания относятся к рефлексам типа (00 l), (0 k 0), (h 00).

Характер погасаний, вызываемый присутствием винтовой оси, также зависит от величины переноса вдоль оси вращения. Пусть ось n -го порялдка параллельна оси Z. При переносе равном ½, 1/3, ¼, 1/6 трансляции с, присутствуют отражения 00 l лишь с l =2 n, 3 n, 4 n, 6 n соответственно.

Таблица. Условия существования рефлексов при наличии винтовых осей.

Винтовая ось	Условие существования рефлексов 00 l
21; 42; 63	l = 2 n
31; 32; 62; 64	l = 3 n
41; 43	l = 4 n
61; 65	l = 6 n

Зональные погасания связаны с присутствием в структуре плоскостей скользящего отражения. Плоскости скользящего отражения осуществляют совместное действие отражения в плоскости и параллельного переноса. Характер погасаний зависит от направления и величины трансляционного переноса. Например, плоскость скользящего отражения, параллельная плоскости XY с переносом равным ½ полной трансляции вызывает погасания по следующим правилам.

Обозначение плоскостей скользящего отражения:

а, b, c – вдоль координатных осей;

n, d – по диагоналям (клиноплоскости)

n – по диагонали нецентрированной грани;

1. Скольжение на ½ полной трансляции направлено вдоль оси Х (а -скольжение) – сохраняются отражения hk 0 лишь с h =2 n

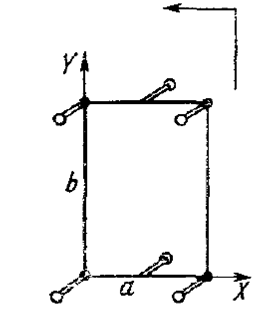
2. Скольжение на ½ полной трансляции направлено вдоль оси Y (b -скольжение) – сохраняются отражения hk 0 лишь с k =2 n

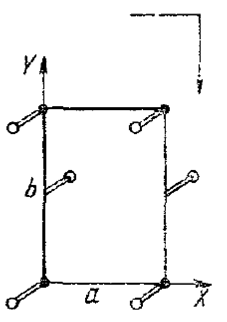
3. Скольжение направлено вдоль диагонали XY (n-скольжение), сохраняются hk0 лишь с h+k=2n (сели величина скольжения равна ½) и h + k =4 n (если сели величина скольжения равна ¼).

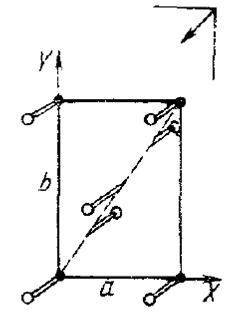
Правила погасаний для плоскостей скользящего отражения, параллельных другим координатным плоскостям, естественно, аналогичны с соответствующей перестановкой индексов.

Таблица. Условия существования рефлексов при наличии плоскостей скользящего отражения.

Плоскость скольжения	Тип рефлекса	Условия наблюдения рефлекса
a	hk0 или h0l	h=2n
b	hk0 или 0kl	k=2n
c	0kl или h0l	l=2n
n	0kl; hk0; h0l	k+l=2n h+k=2n h+l=2n
d	0kl; hk0; h0l	k+l=4n h+k=4n h+l=4n
m (нет скольжения)	Любые	погасаний нет

Дата добавления: 2014-01-07