Кинетические модели Эйгеновского типа

ДОБИОЛОГИЧЕСКАЯ МОЛЕКУЛЯРНАЯ ЭВОЛЮЦИЯ

• Способность генных сетей к самовоспроизведению является фундаментальным свойством, обретенным в ходе добиологической молекулярной эволюции. Однако очевидно, что основные понятия биологической теории эволюции: особь, наследование, наследственная изменчивость, генотип, фенотип, популяция и т.д., в общем случае неприменимы к добиологической эволюции. Поэтому элементарным объектом добиологической эволюции следует считать фракцию макромолекул (полинуклеотидов, полипептидов). От других фракций она должна отличаться последовательностью мономеров и молекулярной функцией.

• Соответственно, в добиологической эволюции элементарной эволюционирующей единицей является устойчивый коллектив (ансамбль) макромолекул, т.е. совокупность фракций макромолекул, которые связаны между собой процессами синтеза (матричного и нематричного), ферментативного катализа, стереохимического взаимодействия, деградации, модификации и т.д.

• Сеть функциональных взаимодействий ансамбля и набор концентраций его молекулярных компонент образует динамическую структуру ансамбля. Эволюцией ансамбля собственно и будет являться изменение его динамической структуры.

• Подобного рода устойчивые ансамбли макромолекул с одной стороны имеют свойства особей (стабильная внутренняя структура, самовоспроизведение) и с другой стороны популяций (способность эволюции путем мутаций и отбора). Устойчивость системы самовоспроизведения определяется ее циклическим характером.

В 1973 г. М. Эйген применил химико-кинетический подход к описанию динамики коллективов информационных макромолекул. Эти модели позволяют описать возможные варианты организации коллективов макромолекул и оценить с эволюционных позиций их свойства, хотя это, вероятно, и не относится к реальному эволюционному процессу

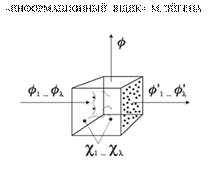
• Будем считать, что процессы матричного синтеза макромолекул далеки от равновесия и протекают только в комплексах матриц (полинуклеотидных) и ферментов, осуществляющих этот синтез. Обозначим x_i — полную концентрацию макромолекул i-го типа, a z_i — концентрацию комплекса (комплексов), производящего макромолекулы i-ro типа.

• где a_i — параметр синтеза, b_i — параметр распада макромолекул i-ro типа, а Ф — единый поток разбавления всех макромолекул, f_i — функция формирования комплексов i -го типа, d_i — константа их дезинтеграции.

• Примем так называемое «селекционное ограничение» — дополнительное требование (в некотором смысле – граничное условие), связанное с регулированием потока Ф. Будем использовать только ограничение, обеспечивающее так называемое постоянство внутренней организации коллектива макромолекул, а именно:

• а) концентрации мономеров нуклеиновых кислот и белков, а также других субстратов в резервуаре избыточны, т. е. параметры а _i, b _i, d _i и функции f _i и Ф не зависят от них;

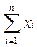• б) суммарная плотность макромолекул С постоянна, т.е.

что достигается регулированием потока разбавления Ф. Это ограничение обусловлено тем, что реальные системы, где может идти синтез макромолекул — клетки, коацерваты — растут или дробятся не переуплотняясь, а это эквивалентно регулированию стока;

• в) механизм разбавления одинаков для всех фракций, что описывается членом -Ф x_i.

• Кроме того, Эйген предполагает, что комплексы z_i квазиравновесны, т. е. равновесие по ним устанавливается значительно быстрее, чем изменяются x _i и поток разбавления. Тогда, полагая dz/dt = 0, получаем систему алгебраических нелинейных уравнений:

d_iz_i , i=1,n

Введенная динамическая система для коллектива макромолекул оказывается полностью эквивалентна уравнениям популяционной генетики. Введем относительные концентрации

u_i = x_i/C

и величины

w_i = a_iz_i/x_i – b_i

которые являются аналогами «селективных ценностей», или приспособленностей отдельных фракций макромолекул.

Усредняя по коллективу, получаем w =

• Это — аналог средней приспособленности коллектива. Тогда система уравнений динамики приобретает хорошо известный из генетики популяций вид

Суммируя по i, получаем, что

w = Ф

т. е. поток разбавления имеет смысл средней приспособленности коллектива макромолекул. Из популяционной генетики известно, что эта величина определяет темп размножения популяции.

Поэтому естественно требовать, чтобы w = Ф > 0 и окончательно получаем

• — аналог уравнений популяционной генетики с отбором. Очевидно, что фракции, для которых w_i < w, уменьшают относительные концентрации, а если w_i > w, то фракции макромолекул растут. Достижение равновесия возможно при достижении внутренне сбалансированного состояния коллектива макромолекул, иногда оно наступает после вытеснения некоторых фракций, имеющих относительную приспособленность меньше средней.

• Однако, в отличие от популяционно-генетических задач, приспособленности здесь не введены как параметры, а получены из кинетических констант и динамических переменных после задания молекулярных процессов в коллективе. Величины w_i в общем случае не константы, а нелинейные функции частот u_i. Поэтому аналог фундаментальной теоремы естественного отбора Фишера (dw/dt≥0) в общем случае не выполняется. Если коллективы внутренне сбалансированы и внешне обособлены от других фракций макромолекул, то их можно считать автономными единицами отбора следующего уровня, пересчитав приспособленности на эти коллективы.

• Возможны и более сложные режимы функционирования описываемой системы.

• Основная проблема, возникающая в связи с анализом систем самовоспроизведения макромолекул, — это проблема их структурной и динамической устойчивости и внутренней сбалансированности.

• Один из способов решения этой проблемы - циклический характер системы самовоспроизведения.

• Эйген предложил вариант циклического коллектива, состоящего из полинуклеотидов и полипептидов (с разделением функций между ними) и назвал эту конструкцию каталитическим гиперциклом с трансляцией. Матрица I_i воспроизводится с помощью белка E_{i -1} и эта матрица кодирует белок E_i, который необходим для воспроизведения матрицы I_i+1. Таким образом, гиперцикл по сути дела является обобщением каталитического цикла белков с отдельной матрицей для каждого звена. При этом подразумевается, что уже существует система генетического кодирования белков и трансляции (I_i → E_i). На рисунке она не показана.

Дата добавления: 2014-01-07