Графический метод решения ЗЛП, особые случаи решения ЗЛП графическим методом

Задача линейного программирования (ЗЛП). Основные свойства, понятия и определения, примеры практического использования

Наиболее изученными задачами оптимизации являются задачи линейного программирования (ЗЛП), для которых разработан универсальный метод решения – симплекс-метод (метод последовательного улучшения плана).

Определение 1. Задача линейного программирования имеет вид:

Найти максимум или минимум линейной функции
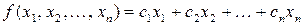
	(6.1)
при линейных ограничениях
	(6.2)
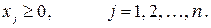
	(6.3)
где 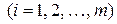, 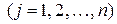– заданные постоянные величины.

Вектор 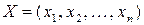называется допустимым решением (допустимым планом) ЗЛП, если его компоненты 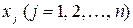удовлетворяют системе ограничений (6.2) и (6.3).

План 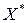называется оптимальным планом (оптимальным решением) ЗЛП, если , т.е. допустимый план, который дает максимум или минимум целевой функции.

Определение 2. Канонической формой записи ЗЛП называется задача вида:

	(6.4)
,	(6.5)
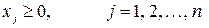,	(6.6)
.	(6.7)
где , , 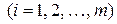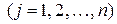– заданные постоянные величины.

Любую ЗЛП можно привести к каноническому виду (КЗЛП). Чтобы неравенства обратились в равенства достаточно:

· в левую часть каждого неравенства со знаком ²≤² ввести добавочную переменную со знаком ²–²;

· в левую часть каждого неравенства со знаком ²³² ввести добавочную переменную со знаком ²+².

Для выработки наглядных представлений о ЗЛП рассмотрим графический метод, который может быть применен в случае решения ЗЛП с двумя переменными:

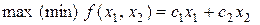
	(7.1)
,	(7.2)
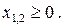
	(7.3)
где 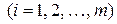, – заданные постоянные величины.

Геометрически ЗЛП представляет собой отыскание в многоугольнике решений такой угловой точки, координаты которой дают максимальное (минимальное) значение линейной целевой функции, причем допустимыми решениями являются все точки многоугольника решений.

Дата добавления: 2014-01-07