Двойственные оценки как мера влияния ограничений на целевую функцию

Теорема об оценках. Значения переменных y_i в оптимальном решении двойственной задачи представляют собой оценки влияния свободных членов b_i системы ограничений (неравенств прямой задачи) на величину :

.

Решая ЗЛП симплексным методом, мы одновременно решаем двойственную задачу. Значения переменных двойственной задачи y_i в оптимальном плане называют, как выше уже отмечено, объективно обусловленными, или двойственными оценками.

Из теоремы об оценках 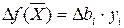известно, что колебание величины b_i приводит к увеличению или уменьшению . Оно определяется величиной y_i в случае, когда при изменении величин b_i значения переменных y_i в оптимальном плане соответствующей двойственной задачи остаются неизменными. Поэтому необходимо найти такие интервалы изменения каждого из свободных членов системы ограничений исходной ЗЛП, в которых оптимальный план двойственной задачи не менялся бы.

Для двойственных оценок оптимального плана весьма существенное значение имеет их предельный характер. Точной мерой влияния ограничений на функционал оценки являются лишь при малом приращении ограничения. Известно, что оценки не меняют своей величины, если не меняется набор векторов, входящих в базис оптимального плана, тогда как интенсивность этих векторов (значения неизвестных) в плане могут меняться.

10. Специальные задачи линейного программирования: транспортная задача, решение средствами MS Excel

Транспортная задача является одной из наиболее распространенных задач линейного программирования и находит широкое практическое приложение.

Постановка задачи (об оптимальном закреплении потребителей к поставщикам). Некоторый однородный продукт, сосредоточенный у m производителей (поставщиков) A_i в количестве a_i 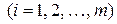единиц, необходимо доставить n потребителям B_j в количестве b_j 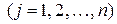единиц. Известна стоимость c_ij перевозки единицы груза от поставщика i к потребителю j. Необходимо составить план перевозок, позволяющий с минимальными затратами перевезти все грузы и полностью удовлетворить потребителей.

Часто исходные данные транспортной задачи записывают в виде таблицы (матрицы) планирования:

Потребитель Производитель	B 1	B 2	¼	B n	Предложение (запасы)
A 1	c 11	c 12	¼	c 1n	a 1
A 2	c 21	c 22	¼	c 2n	a 2
¼	¼	¼	¼	¼	¼
A m	c m1	c m2	¼	c mn	a m
Потребность (спрос)	b 1	b 2	¼	b n

Составим экономико-математическую модель (транспортная задача относится к двухиндексным задачам линейного программирования):

1) вводим переменные: 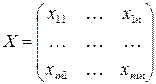, где x_ij – количество единиц груза, перевозимых от поставщика i 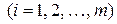к потребителю j 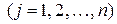; стоимость этой перевозки составит ;

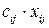2) задаем целевую функцию 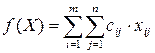, которая выражает стоимость перевозок всех грузов;

3) из условий задачи составляем ограничения:

a) все грузы должны быть перевезены, т.е.

;

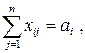
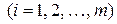b) все потребности должны быть удовлетворены, т.е.

.

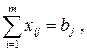
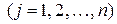Таким образом, модель транспортной задачи имеет следующий вид:

Найти минимальное значение целевой функции
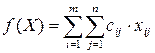
	(10.1)
при ограничениях
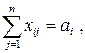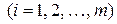,	(10.2)
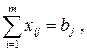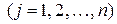,	(10.3)
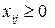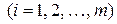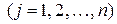, , .	(10.4)

В рассмотренной модели предполагается, что суммарные запасы равны суммарным потребностям, т.е.

.

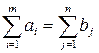(10.5)

Транспортная задача, в которой суммарные запасы и суммарные потребности совпадают, называется закрытой транспортной задачей, в противном случае получаем открытую транспортную задачу.

Замечание. Решение открытой ТЗ проводится сведением к закрытой ТЗ (введением фиктивного поставщика или фиктивного потребителя):

a) если суммарные запасы превышают суммарные потребности, то вводится фиктивный потребитель B _n+1, потребность которого равна ;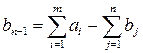

b) если суммарные потребности превышают суммарные запасы, то вводится фиктивный поставщик A _m+1, запасы которого равны .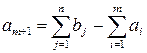

Стоимость перевозки единицы груза до фиктивного потребителя или от фиктивного поставщика приравнивается нулю, так как груз в обоих случаях фактически не перевозится.

11. Специальные задачи линейного программирования: задача о назначениях, решение средствами MS Excel

Задача о назначениях является частным случаем транспортной задачи, в котором все значения a_i 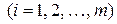и b_j 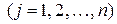равны 1. Такая задача возникает при распределении людей на должности или работы, водителей на машины, рабочих на станки, автомашин на маршруты, групп по аудиториям и т.п.

Постановка задачи (об оптимальном закреплении исполнителей на работы). Имеется n видов работ и n исполнителей этих работ. Известна эффективность c_ij выполнения исполнителем i работы j. Требуется так назначить исполнителей по видам работ, чтобы суммарный эффект от назначений был максимальным.

Часто исходные данные задачи о назначениях записывают в виде таблицы (матрицы) планирования:

Работы Исполнители	B 1	B 2	¼	B n	Число исполнителей
A 1	c 11	c 12	¼	c 1n
A 2	c 21	c 22	¼	c 2n
¼	¼	¼	¼	¼	¼
A n	c n1	c n2	¼	c nn
Количество работ			¼

Составим экономико-математическую модель (задача о назначениях относится к двухиндексным задачам линейного программирования):

1) вводим переменны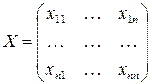е: , где

2) задаем целевую функцию 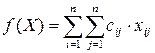, которая выражает суммарный эффект от назначений;

3) из условий задачи составляем ограничения:

a) каждый исполнитель должен быть назначен на работу, т.е.

;

b) на каждую работу должен быть назначен исполнитель, т.е.

.

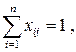
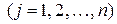Таким образом, модель задачи о назначениях имеет следующий вид:

Найти минимальное значение целевой функции
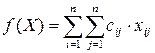
	(11.1)
при ограничениях
,	(11.2)
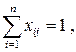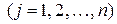,	(11.3)
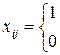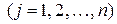, , .	(11.4)

Замечание. Если число исполнителей m не равно числу работ n (т.е. задача является открытой), то возможно применение двух способов:

1) решение открытой задачи о назначениях сводим к решению закрытой задачи о назначениях; для этого вводим фиктивных исполнителей или фиктивные виды работ;

2) изменяем ограничения 11.2 и 11.3:

a) если число исполнителей m больше числа работ n, то

; ;

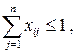
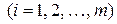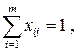
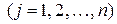b) если число исполнителей m меньше числа работ n, то

; .

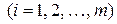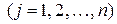Дата добавления: 2014-01-07