Метод динамического программирования

Решение средствами MS Excel

При решении ЗНЛП в диалоговом окне Поиск решения во вкладке Параметры должна быть отключена опция Линейная модель.

Для решения некоторых типов задач оптимального программирования используется метод динамического программирования (ДП).

В основе общей концепции метода ДП лежит принцип оптимальности Беллмана: ²Оптимальное поведение обладает тем свойством, что, каковы бы ни были первоначальное состояние и решение в начальный момент, последующие решения должны составлять оптимальное поведение относительно состояния, получающегося в результате первого решения².

Благодаря принципу оптимальности удается при последующих переходах испытывать не все возможные варианты, а лишь оптимальные выходы.

Для решения задач методом динамического программирования не предлагается подходящих программных средств – разобраться в сути принцип оптимальности Беллмана следует ²с карандашом в руке² [1, с.96-102].

Тема 4: Оптимальные решения для отдельных классов задач оптимизации в экономике

15. Методы теории массового обслуживания: основные понятия и определения, примеры СМО

При решении многих задач оптимальной организации торговли, бытового обслуживания, складского хозяйства и т.п. часто используется интерпретация производственной структуры как системы массового обслуживания (СМО), т.е.системы в которой с одной стороны, постоянно возникают запросы на выполнение каких-либо работ, а с другой стороны происходит постоянное удовлетворение этих запросов.

Всякая СМО включает 4 элемента:

1) источник требований (ИТ);

2) входящий поток требований;

3) система обслуживания, которая включает в себя:

· очередь,

· обслуживающее устройство (каналы обслуживания);

4) выходящий поток требований.

Требованием называется каждый отдельный запрос на выполнение какой-либо работы. Поступив в обслуживающую систему, требование (заявка) на обслуживание присоединяется к очереди других ранее поступивших требований и ждет обслуживания. Блок обслуживания выбирает очередное требование и начинает его обслуживать. После завершения обслуживания обслуживающая система приступает к обслуживанию следующего требования. Этот цикл работы СМО многократно повторяется.

К основным характеристикам СМО относятся:

· среднее число заявок находящихся в системе;

· среднее число заявок в очереди (ее длина);

· средняя продолжительность пребывания клиента в системе;

· средняя продолжительность пребывания клиента в очереди;

· среднее количество занятых средств обслуживания;

· среднее время обслуживания;

· вероятность отказа в обслуживании и др.

Для классификации СМО используется ряд признаков:

1. В зависимости от условий ожидания начала обслуживания различают:

· СМО с отказами (потерями) – требования получившие отказ (каналы заняты) теряются;

· СМО с ожиданием - требования становятся в очередь и ожидают обслуживания, такие СМО делятся на:

o СМО с ограниченной длиной очереди;

o СМО с неограниченной длиной очереди;

o СМО с ограниченным временем ожидания.

2. По числу каналов обслуживания различают два вида СМО:

· одноканальные;

· многоканальные.

3. По месту нахождения источника требования (ИТ) СМО делятся на два вида:

· разомкнутые – ИТ вне системы;

· замкнутые – ИТ в составе системы.

4. По дисциплине обслуживания (в зависимости от порядка выбора заявок на обслуживание) выделяют:

· СМО с приоритетом – вначале обслуживаются заявки с более высоким приоритетом;

· СМО без приоритета – приоритет в обслуживании заявок отсутствует.

Методы и модели исследования СМО можно разделить на

· аналитические;

· статистические.

Аналитические методы позволяют получить характеристики СМО как функции её параметров, но применимы эти методы к ограниченному кругу задач теории массового обслуживания (ТМО).

Простейший поток требований

В настоящее время достаточно хорошо разработана ТМО применительно к простейшему (Пуассоновскому) потоку заявок на обслуживание.

Для простейшего потока частота поступления требований в систему подчиняется закону Пуассона, то есть вероятность поступления за время t ровно k требований задается формулой , где λ – параметр потока (число требований, поступающих в единицу времени).

Основные свойства простейшего потока:

Ординарность – практическая невозможность одновременного поступления двух и более требований.

Стационарность – означает, что среднее число требований (математическое ожидание) поступающих в систему в ед. времени (λ=const) не меняется во времени.

Отсутствие последействия – число требований, поступивших в систему до момента времени t не определяет того, сколько требований поступит в систему за промежуток времени от t до t + Δ t.

Время обслуживания требований в системе

Важной характеристикой СМО является время обслуживания одного требования в системе. Оно является случайной величиной и может быть описано законом распределения.

Наиболее часто рассматривается как случайная величина (СВ), которая подчиняется экспоненциальному закону распределения.

Для этого закона функция распределения вероятности имеет вид: , т.е. вероятность того, что время обслуживания не превосходит некоторой величины t, определяется формулой , где μ – параметр экспоненциального закона распределения времени обслуживания требований в системе – т.е. величина, обратная среднему времени обслуживания одного требования 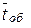, т.е. .

Дата добавления: 2014-01-07