Картографические проекции и искажения на картах

Картографическая проекция — это математически определен­ное отображение поверхности эллипсоида или шара на плоскости карты.

Проекция устанавливает однозначное соответствие между гео­дезическими координатами точек (широтой В и долготой L) и их прямоугольными координатами (X и Y) на карте. Уравнения про­екций в общей форме выглядят предельно просто

X = f ₁(B, L); Y = f ₂(B, L).

Конкретные реализации функций f ₁ и f ₂ часто выражены до­вольно сложными математическими зависимостями, их число бес­конечно, а следовательно, разнообразие картографических проек­ций практически неограниченно.

Теория картографических проекций составляет главное содер­жание математической картографии. В этом разделе разрабатывают методы изыскания новых проекций для разных территорий и раз­ных задач, создают приемы и алгоритмы анализа проекций, оцен­ки распределения и величин искажений. Особый круг задач связан с учетом этих искажений при измерениях по картам, переходом из одной проекции в другую и т. п. Компьютерные технологии позво­ляют рассчитывать проекции с заданными свойствами.

Исходная аксиома при изыскании любых картографических про­екций состоит в том, что сферическую поверхность земного шара (эллипсоида) нельзя развернуть на плоскости карты без искажений. Неизбежно возникают деформации — сжатия и растяжения, раз­личные по величине и направлению. Именно поэтому на карте воз­никает непостоянство масштабов длин и площадей.

Иногда искажения картографических проекций очень замет­ны, например очертания материков выглядят непривычно вытя­нутыми или сплющенными, а другие части изображения стано­вятся раздутыми. Искажаются не только размеры, но и формы объектов. В картографических проекциях могут присутствовать следую­щие виды искажений:

• искажения длин— вследствие этого масштаб карты непосто­янен в разных точках и по разным направлениям, а длины линий и расстояния искажены;

• искажения площадей — масштаб площадей в разных точках карты различен, что является прямым следствием искаже­ний длин и нарушает размеры объектов;

• искажения углов — углы между направлениями на карте ис­кажены относительно тех же углов на местности;

• искаженияформ — фигуры на карте деформированы и не подобны фигурам на местности, что прямо связано с иска­жениями углов.

Любая бесконечно малая окружность на шаре (эллипсоиде) предстает на карте бесконечно малым эллипсом — его называют эллипсом искажений. Для наглядности вместо бесконечно малого эллипса обычно рассматривают эллипс конечных размеров (рис. 2.1).

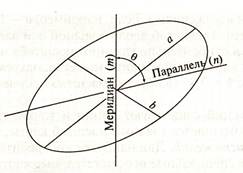
Рис. 2.1. Эллипс искажений, характеризующий искажения масштабов в данной точке (в центре эллипса):

а— направление наибольшего растяжения масштаба; 6— направление наи­большего сжатия масштаба; т — масштаб по меридиану; п — масштаб по параллели.

Его размеры и форма отражают искажения длин, площадей и уг­лов, а ориентировка большой оси относительно меридиана и па­раллели — направление наибольшего растяжения. Большая ось эл­липса искажений характеризует наибольшее растяжение в данной точке, а малая ось — наибольшее сжатие, отрезки вдоль меридиа­на и параллели соответственно характеризуют частные масштабы по меридиану т и параллели п. Определив значения т и п, а также измерив угол θ, под кото­рым пересекаются на карте меридиан и параллель, можно затем рассчитать значения наибольшего а и наименьшего в частных мас­штабов длин, частный масштаб площадей р в данной точке, а также значение искажения углов со по формулам:

р = т п sin θ;

а + b= 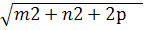; а – b = ;

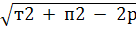Если главные оси эллипса ориентированы по меридиану и па­раллели, то

а = т и b = п либо а = п и b = т,

р = тп,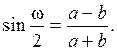

Значения т, п, а, b и р измеряют в процентах или в долях от главного масштаба. Например, если а = 1,12, то это означает, что частный масштаб по направлению большой оси эллипса искаже­ний составляет 1,12 (или 112%) от главного масштаба. Иногда в качестве показателей искажений используют их отклонения от еди­ницы: т – 1, п – 1, а – 1, b – 1 и р – 1 — эти показатели называ­ют относительными искажениями. Если, например, а – 1 = 0,12, то это значит, что частный масштаб вдоль большой оси эллипса искажений преувеличен относительно главного масштаба на 0,12 (или на 12%). Частный масштаб может оказаться и меньше глав­ного, например b = 0,85 (85%), т.е. масштаб преуменьшен на 0,15 (на 15%).

В ряде проекций существуют линии и точки, где искажения отсутствуют и сохраняется главный масштаб карты — это линии и точки нулевых искажений. Для наиболее употребительных проек­ций существуют специальные вспомогательные карты, на которых показаны эти линии и точки, а кроме того проведены изоколы— линии равных искажений длин, площадей, углов или форм. При определении размеров искажений в заданной точке можно вос­пользоваться картами изокол либо провести несложные измере­ния, а затем — вычисления по приведенным выше формулам.

Дата добавления: 2014-01-07