Механика твердого тела

Кинетическая энергия вращения. Момент инерции материальной точки и тела относительно неподвижной оси.

Пусть материальная точка массой m движется вокруг некоторой оси по окружности радиуса r со скоростью υ. Тогда кинетическую энергию точки с учетом связи линейной и угловой скоростей υ =ω·r можно записать так:

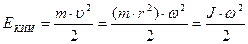, где величина J=m·r² называется моментом инерции материальной точки.

Моментом инерции тела относительно оси называется сумма моментов инерции эле­ментов (материальных точек), из которых состо­ит тело: .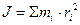

Момент инерции сплошного тела определя­ют интегрированием по всему объему (по всем материальным точкам): .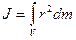

Если тело имеет плотность ρ, то последнее равенство можно представить в виде:

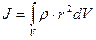, где учтено, что d т= ρ·dV.

Момент инерции сплошного цилиндра мас­сой т и радиуса основания R относительно оси, проходящей через центр масс цилиндра па­раллельно его образующей, рассчитанный по этой формуле, равен: .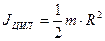

Для сплошного шара массой т и радиуса R момент инерции относительно оси, проходящей через центр масс шара, равен: .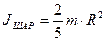

Момент инерции для стержня длиной ℓ и массой т относительно оси, проходящей через центр масс стержня перпендикулярно ему,: .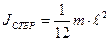

Момент инерции J тела характеризует, с одной стороны, инертные свойства тела при вращательном движе­нии, а с другой стороны, распределение вещества в пространстве относительно оси. Момент инерции, так же как и масса тела, является ад­дитивной величиной.

Если известен момент инерции J_o тела от­носительно оси, проходящей через центр масс тела, то можно найти его момент инер­ции относительно любой другой параллельной ей оси: J = J₀ + m·d ², где d – расстояние между осями.

Последнее равенство выражает теорему Штейнера: момент инерции относительно любой оси вра­щения равен моменту инерции относительно параллельной оси, проходящей через центр масс, сложенному с произведением массы тела на квадрат расстояния центра масс тела от оси вращения.

Из теоремы Штейнера очевидно, что всег­да J>J₀, т.е. минимальное значение момента инерции до­стигается для оси, проходящей через центр масс.

Единицей момента инерции в системе СИ служит 1 кг·м².

Если тело катится, то кинетическая энергия такого тела определяется поступательным движением тела как целого и вращением относительно движущейся оси:

.

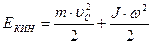Дата добавления: 2014-01-07