Элементы комбинаторики

Лекция 1.

Комбинаторика – раздел дискретной математики, в котором изучаются методы подсчета количества комбинаций элементов различных множеств.

1. Правило произведения. Рассмотрим последовательность элементов 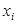длиной 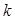: (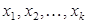) – строка. Две строки (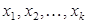), ) 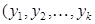будем считать различными, если они отличаются хотя бы одним элементом.

Пусть элемент 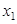может быть выбран 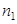способом; при каждом выборе 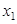элемент 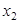может быть выбран 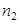способами; при каждом выборе пары 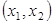элемент 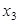может быть выбран 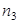способами и т.д. при каждом выборе строки 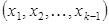элемент 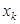может быть выбран 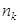способами. Тогда число различных строк 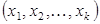равно произведению .

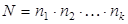Пример 1. Сколько существует трехзначных номеров, не содержащих цифры 3?

Решение. Трехзначное число можно представить как строку 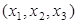. На место 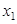можно поставить цифры 1,2,4,5,6,7,8,9, т.е. всего 8 цифр, 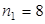. На место 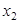: 0,1,2,4,5,6,7,8,9, 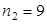, аналогично, на место 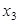: 0,1,2,4,5,6,7,8,9, 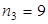. Число трехзначных номеров, не содержащих цифру 3, равно .

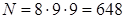Пример 2. Сколько различных подмножеств имеет множество 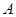, состоящее из 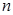элементов?

Решение. Пусть 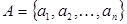. Пусть 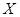- подмножество в 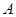: 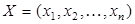. Обозначим 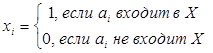, т.е., например, 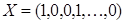. Следовательно, 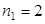, ,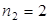…, 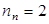. Следовательно, .

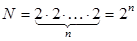2. Размещения. Размещениями (без повторений) из 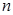элементов по 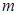называются упорядоченные наборы из 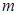элементов, взятых из данных 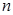. Размещения отличаются составом элементов или их порядком. Число размещений определяется формулой

,

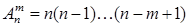или

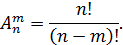
Пример. Сколькими различными способами можно выбрать три лица из десяти кандидатов на три различные должности?

Решение. Кандидатов, претендующих на первую должность, будем ставить на первое место, на вторую должность – на второе место, на третью должность – на третье место. Наборы кандидатов зависят от состава и порядка, следовательно, являются размещениями из десяти по три, их количество находим по формуле: .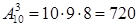

3. Размещения (c повторениями). Отображение множества 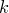первых натуральных чисел 1,2,…,m в данное множество 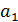,…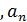называется размещением с повторениями, составленным из данных n элементов по m.

Два размещения с повторениями одинаковы тогда и только тогда, когда на одинаковых местах находятся одни и те же элементы.

Если в размещении с повторениями некоторый элемент ставится в соответствие 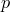различным натуральным числам, т.е., иначе говоря, данный элемент занимает 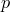различных мест, то говорят, что этот элемент повторяется в размещении 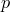раз.

Число размещений из 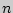элементов по 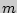с повторениями обозначается 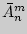и находится как

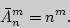
Пример 1. Всевозможные размещения с повторениями из трех элементов 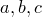по 2:

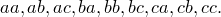
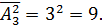
Пример 2. Сколько существует различных трехзначных чисел, в записи которых используются только цифры 1, 2, 3, 4, 5?

Решение: m=3, n=5,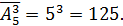

4. Перестановки. Перестановками (без повторений) элементов множества называются упорядоченные наборы из всех элементов множества. Перестановки не отличаются составом, а отличаются только порядком элементов в них. Число перестановок определяется формулой

.

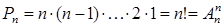Пример. Сколькими различными способами на скамейке можно посадить 6 человек?

Решение. Наборы не отличаются составом, а только порядком, являются перестановками из 6 элементов, их количество определяется формулой

.

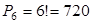5. Перестановки (c повторениями). Число перестановок ,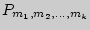

в которых 1-й элемент повторяется 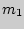раз, 2-й - 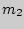раз, а 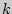-й - 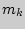раз, находится следующим образом:

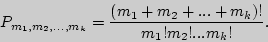
Пример. Сколько "слов" можно получить, переставляя буквы в слове МАТЕМАТИКА?

Решение. Заметим, что если бы все буквы были различны, то получили бы 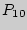новых "слов", но буква "М" употребляется в "слове" 2 раза, "А" - 3 раза, "Т" - 2 раза, оставшиеся три буквы - по разу.

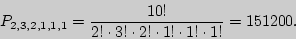
6. Сочетания. Сочетаниями (без повторений) из 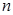элементов по 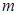называются неупорядоченные наборы по 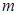элементов, взятых из данных 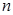. Сочетания отличаются только составом. Число сочетаний определяется формулой

.

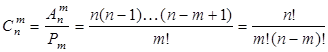Пример. Сколькими способами можно выбрать три лица из десяти кандидатов на три одинаковые должности?

Решение. Наборы определяются только составом, являются сочетаниями из 10 по 3:

.

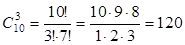1.7. Сочетания ( с повторениями). Число сочетаний с повторениями 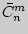из 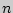элементов по 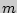выражается через число сочетаний без повторений:

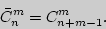
Пример. В кафе в продаже имеются 5 сортов пирожных. Сколькими способами 8 студенток могут заказать себе по одному пирожному?

Решение. Зашифруем каждую покупку 8 пирожных единицами по 5 сортам, разделяя сорта нулями. Тогда каждой покупке будет соответствовать упорядоченный набор из 8 единиц и 4 (= 5 - 1) разделительных нулей, а общее число покупок будет соответствовать числу перестановок этих нулей и единиц. Таким образом,

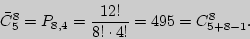
1) 1 2 3 4 5

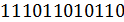
2) 1 2 3 4 5

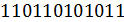
Свойства числа сочетаний:

1..

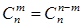2..

3..

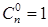4..

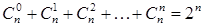5.

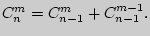
Дата добавления: 2014-01-07