Гармонический анализ непериодических колебаний

Аналитическое описание непериодических колебаний

Пусть имеется периодическое колебание, изображенное на рис. 36. Потребуем, чтобы период T→∞, тогда периодическое колебание обращается в непериодическое.

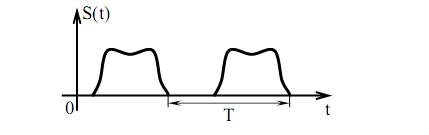
Рис. 36. Периодическое колебание

Подставим выражение для коэффициентов C_n в ряд Фурье, записанный в комплексной форме, с учётом того, что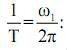

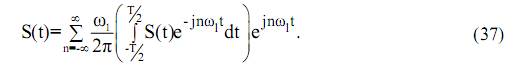
Так как T→∞ и 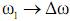, то знак суммы обращается в знак интегрирования, а 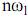– в текущее значение частоты 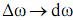, тогда

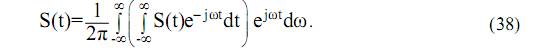
Выражение, входящее под скобки называется спектральной плотностью сигнала и обозначается S(jω). Перепишем (38) в виде системы:

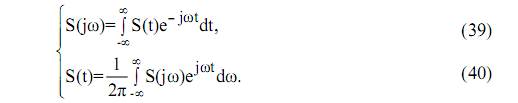
Эти соотношения называется парой преобразований Фурье. Переход от временного представления колебания в частотную область определяет прямое преобразование Фурье, а переход от частного представления к временному – обратное преобразование Фурье.

Для спектральной функции S(jω) справедливы известные представления в тригонометрической и комплексной формах

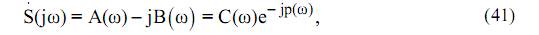
где A(ω) и B(ω) – чётная (косинусоидальная) и нечётная (синусоидальная) составляющие спектральной плоскости;

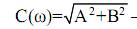амплитудно-частотная характеристика колебания (АЧХК);

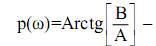– фазо-частотная характеристика колебания (ФЧХК).

Следует учесть, что ArctgX = arctgX ± πN, где N – целое число.

Рассмотрим пример. Необходимо определить спектральную плотность и построить графики АЧХК и ФЧХК импульса с амплитудой Е и длительностью τ (рис. 37).

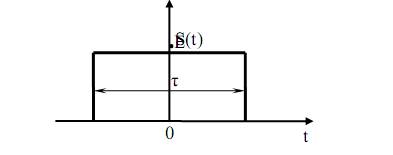
Рис. 37. Прямоугольный импульс

Используя (18) получим

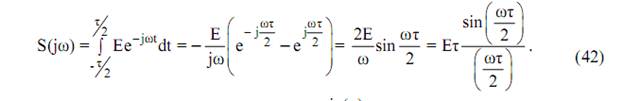
Выражение (42) представлено в виде функции 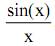, предел от которой при х стремящимся к нулю равен единице (первый замечательный предел).

Построим графики АЧХК и ФЧХК согласно (42). На рис. 38 приведена спектральная характеристика импульсного колебания, а также АЧХК – рис. 39, ФЧХК – рис. 40.

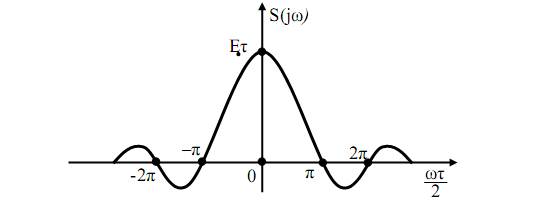
Рис. 38. Спектральная характеристика импульса

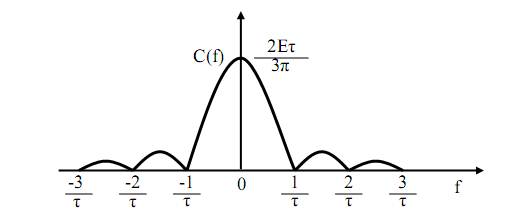
Рис. 39. АЧХК

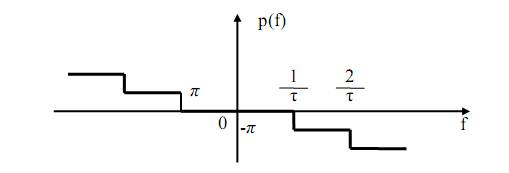
Рис. 40. ФЧХК

В сравнении с периодическим колебанием непериодическое имеет плотное расположение спектральных линий, поэтому введено понятие спектральной плотности. Если амплитуда колебания измеряется в вольтах, то спектральная плотность в В/Гц или В*с. Первый нуль спектральной плотности приходится на точку 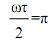, откуда несложно получить, что .

Анализ распределения энергии такого колебания в частотной области показывает, что 90% приходится на основной лепесток спектральной плотности и лишь 10% занимает энергия затухающих осциллирующих лепестков.

Дата добавления: 2014-01-07