
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Принцип перестановочной двойственности
Проведем сравнение первого и второго, а также третьего и четвертого уравнений Максвелла на предмет их симметрии. Видно, что для того, чтобы они стали симметричными необходимо дополнить второе уравнение некоторой фиктивной плотностью магнитного тока, а четвертое уравнение – фиктивной объемной плотностью заряда

получим второе уравнение.
Производя замену в третьем уравнении Максвелла типа
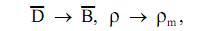
получим четвертое уравнение.
Дополняя рассуждения симметрией материальных уравнений можно ввести принцип перестановочной двойственности
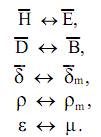
Такой подход позволяет упростить решение ряда электродинамических задач.
Так, при известном решении относительно одного вектора электромагнитного поля можно сразу найти решение для другого или зная описание параметров одного типа среды представить параметры среды другого сорта.
|
Дата добавления: 2014-01-07; Просмотров: 1224; Нарушение авторских прав?; Мы поможем в написании вашей работы!