Поляризация волн

Ориентация вектора электрической напряженности поля в пространстве в выбранной системе координат определяет поляризацию ЭМВ.

Если некоторый вектор изменяется во времени и пространстве по закону

и не изменяет своего направления в пространстве, то имеет место линейная поляризация.

Когда вектор s(z, t) коллиниарен оси х и в любой точке плоскости x0z ортогонален оси 0z, то этот вид линейной поляризации называют вертикальной. Такую поляризацию можно сформировать, например с помощью вертикального вибратора заданной длины (рис. 80).

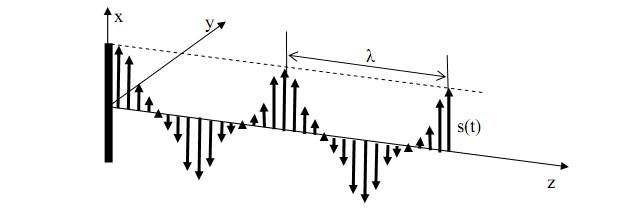
Рис. 80. Вертикальная поляризация волны

Когда вектор s(z, t) коллиниарен оси у и в любой точке плоскости у0z ортогонален оси 0z, то поляризацию называют линейной горизонтальной (рис. 81).

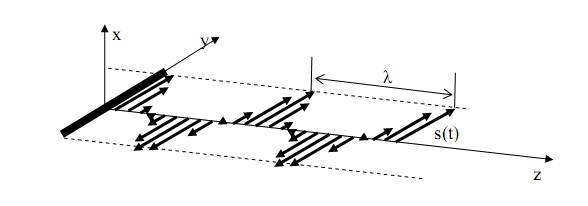
Рис. 81. Горизонтальная поляризация волны

При этом будем считать, что они формируются двумя электрическими вибраторами одинаковой длины с токами Ix и Iу, расположенными в фиксированной точке z = 0 (рис. 82).

Рис. 82. Волна правой поляризации

Результатом сложения двух волн является

и суммарный вектор оказывается линейно поляризованным, а его наклон в плоскости х0у определяется соотношением амплитуд s₁ и s₂.

Если s ₂ = 0, то поляризация является вертикальной. Когда s₁ = 0, то имеет место горизонтальная поляризация волны.

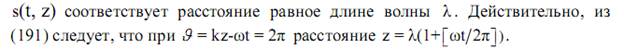
Если амплитудные значения s₁ и s₂ равны, то конец суммарного вектора движется по кругу, радиусом s₁, описывая в пространстве спиралевидную траекторию правого вращения (рис. 83). Такая поляризация волны называется поляризацией правого вращения или правой.

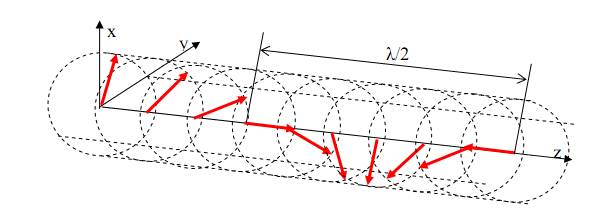
Рис. 83. Траектория правой волны

Волна с круговой поляризацией может быть сформирована за счет изменения другой компоненты аргумента колеблющейся функции

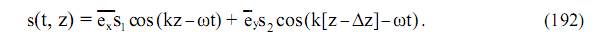
Если амплитудные значения s₁ и s₂ равны, то суммарный вектор движется по кругу, радиусом s₁, против часовой стрелки по спирали (рис. 84). Такая поляризация волны называется поляризацией левого вращения или левой.

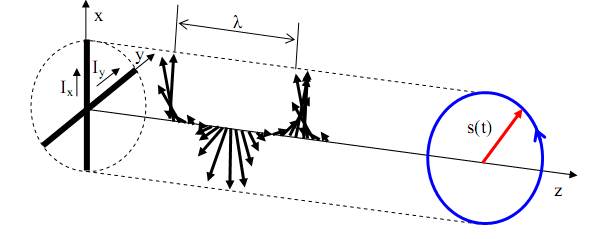
Рис. 84. Волна левой поляризации

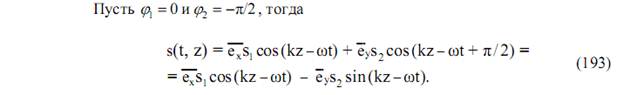
Оценим каким должно быть смещение формирователей поля относительно друг друга, совещаясь вышеприведенными размышлениями по созданию волн круговой поляризации. При фиксированной частоте потребуем 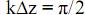, тогда 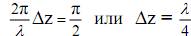, следовательно фазировку можно осуществлять разносом вибраторов в пространстве при условии идентичности напряженностей поля (рис. 85).

Рис. 85. Формирование правой волны за счет дистанционного

разноса источников

Можно обеспечить крен результирующего вектора электрической напряженности поля за счет создания дополнительного поля по оси 0z (рис. 86):

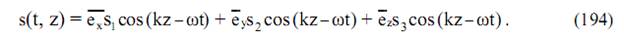
Реально ситуация, связанная с наклоном фронта вертикально поляризованной волны, возникает за счет рефракции, которая проявляется из-за отличия плотностей слоев атмосферы. Нижние слои атмосферы являются самыми плотными, верхние менее плотные. В результате происходит наклонение фронта волны, до тех пор пака он не станет соответствовать изгибу Земли (т.е. станет горизонтально поляризованной).

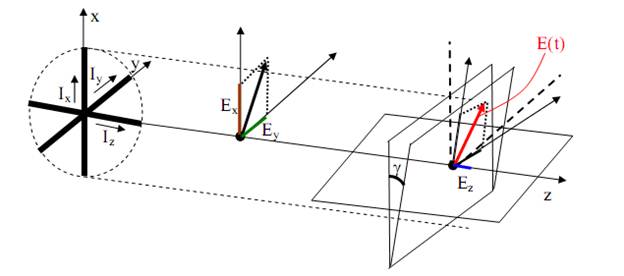
Рис. 86. Формирование крена фронта волны

При различных амплитудах формируемого поля можно трансформировать вид поляризации. При этом обобщенно следует говорить об эллиптической форме поперечного сечения траектории движения вектора электрической напряженности поля (рис. 87, а), т.е об эллиптической поляризации волны. Таким образом, на формирование поляризационной структуры волны существенную роль оказывает соотношение амплитуд поля двух линейных вибраторов

Данное уравнение является уравнением эллипса, вписанного в прямоугольник со сторонами 2s₁ × 2s₂.

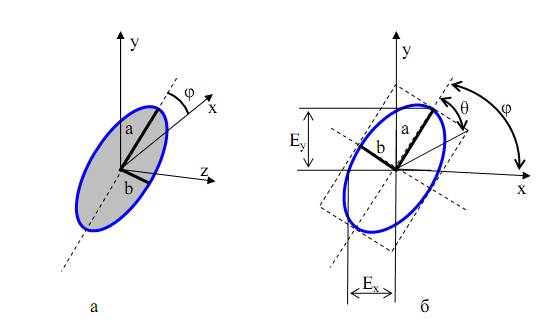
Рис. 87. Эллиптически поляризованная ЭМВ:

а –поперечное сечение; б – параметры

Для оценки вида или степени поляризации вводят понятие коэффициента эллиптичности, под которым понимают отношение малой b и большой а полуосей эллипса (рис. 87, б).

В принятой геометрии отсчитывают угол φ, который характеризует преимущественную поляризацию ЭМВ. Таким образом, 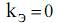при линейной, 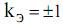при левой (+) и правой (–) круговых поляризациях, промежуточным значениям соответствует эллиптическая поляризация.

Другим параметром является угол эллиптичности

который характеризует пространственную ориентацию главной оси эллипса при трансформациях прямоугольника в который он вписан.

Рассмотрим случай, когда горизонтальный вибратор смещен относительно оси 0у на некоторый угол ξ (рис. 88). Очевидно, что такое положение приведет к изменению поперечных проекций вектора электрической напряженности и как следствие наклон суммарного вектора. При фазировке, соответствующей созданию круговой поляризации, происходит преобразование круга в эллипс. Таким образом, ошибки пространственных смещений формирующих источников будут всегда приводить к эллиптической поляризации ЭМВ.

Рис. 88. Влияние пространственных смещений источников

на формирование поляризации:

а – источники; б – проекции вектора Е при смещении источников;

в – проекции вектора Е без смещении источников (для сравнения)

Дата добавления: 2014-01-07