План лекции. 1. Проекция силы на ось и плоскость

1. Проекция силы на ось и плоскость.

2. Аналитический способ задания и сложения сил.

3. Момент силы и момент пары.

4. Теорема Вариньона.

5. Теорема о параллельном переносе сил.

6. Приведение пространственной системы сил к данному центру.

Краткое содержание лекции

Проекцией силы на ось называется скалярная величина, равная длине отрезка, заключенного между проекциями начала и конца силы. Она равна произведению модулясилы F на косинус угла a между направлением силы и положительным направлением оси

. (2.1)

Аналогично определяется проекция силы на плоскость, но она уже является вектором:

. (2.2)

Если плоскость ху связать с декартовой системой координат, то можно получить формулы для разложения сил по осям:

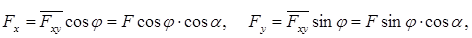
(2.3)

где a - угол между силой и плоскостью ху;

j - уголь между положительным направлением оси х и вектором .

Аналитический способ задания силы заключается в задании координат точек приложения 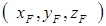и проекции на оси координат - . В этом случае модуль силы равен

, (2.4)

а углы между силой и осями координат определяются из выражений

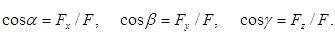(2.5)

Геометрическую сумму системы сил называют главным вектором этой системы – R.

Пусть задана система сил , имеющая равнодействующую , то есть .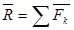

По этой теореме:

(2.6)

Тогда

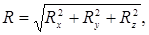(2.7)

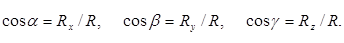(2.8)

Моментом силы относительно точки (центра) называют меру механического воздействия, учитывающую положение силы по отношению к точке и выражающуюся произведением модуля силы на плечо, взятым со знаком плюс или минус. Точку, относительно которой определен момент силы, называют центром момента. Опущенный из центра момента перпендикуляр на линию действия силы является плечом силы. Знак момента силы определяется по следующему правилу: момент считается положительным, когда сила стремится повернуть тело вокруг центра против хода часовой стрелки, когда по ходу часовой стрелки – отрицательным.

. (2.9)

Отметим следующие свойства момента силы относительно центра:

1) момент силы относительно точки не изменяется при переносе силы вдоль ее линии действия, так как при этом не меняется плечо силы;

2) момент силы относительно точки равен нулю, когда линия действия силы проходит через эту точку (плечо силы равно нулю).

Чтобы определить момент силы относительно оси необходимо:

1) провести через произвольную точку О оси плоскость П, перпендикулярную оси;

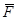2) найти проекцию силы на плоскость П;

3) определить плечо h силы относительно точки О;

4) вычислить произведение ;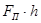

5) определить знак момента: принимаем его со знаком плюс, если с положительного конца оси поворот, который стремится совершить сила , виден против хода часовой стрелки, и со знаком минус – когда по ходу часовой стрелки (рис.1.3)

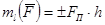. (2.10)

Момент силы относительно оси равен нулю: 1) если сила параллельна заданной оси; 2) если линия действия силы пересекает ось.

Парой сил называется система двух равных по модулю параллельных сил, направленных в противоположные стороны. Сумма сил пары равна нулю, но пара сил не уравновешена. Кратчайшее расстояние между линиями действия сил пары называется плечом пары сил. Плоскость, в которой действуют силы пары, называется плоскостью действия пары сил. Совокупность нескольких пар сил, действующих на тело, называется системой пар сил. Пара сил не приводится к равнодействующей. Действие пары на твердое тело сводится к вращательному эффекту, мерой которого является векторная величина, называемая моментом пары сил. Модуль этого вектора равен произведению модуля силы пары на ее плечо, т.е.

Основные свойства пары сил: 1) пару сил можно переносить куда угодно в плоскости действия пары; 2) пару можно переносить из данной плоскости в любую плоскость, параллельную данной; 3) у данной пары можно произвольно менять модули сил и длину плеча, сохраняя неизменным ее момент.

Пары сил эквивалентны, если равны векторы-моменты этих пар. Если на тело действует несколько пар с моментами , то их совокупное воздействие на тело эквивалентно одной паре с моментом , который называют главным моментом.

Рассмотрим несколько важных теорем статики. Теорема Вариньона: момент равнодействующей плоской системы сходящихся сил относительно любого центра равен алгебраической сумме моментов слагаемых сил относительно того же центра. Пусть 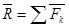, тогда

. (2.11)

Эта теорема справедлива и для моментов относительно любой оси

.

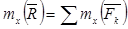Теорема о параллельном переносе. Силу, приложенную к твердому телу, можно, не изменяя ее действия, перенести параллельно самой себе в любую точку тела, прибавляя при этом пару с моментом, равным моменту переносимой силы относительно точки, в которую она переносится.

Точку, к которой приводят систему сил, называют центром приведения данной системы сил.

Теорема. Произвольную систему сил, действующих на твердое тело, можно привести к какому-либо центру, заменив все действующие силы одной силой, равной главному вектору системы сил, приложенному в этом центре, и одной парой сил с моментом, равным главному моменту системы сил относительно того же центра (метод Пуансо).

Главный вектор и главный момент обычно определят аналитически, то есть их проекциями на оси координат. Проекции главного момента также определяются по теореме о проекциях суммы векторов на ось:

Таким образом, для задания произвольной системы сил достаточно задать главный вектор и главный момент относительно любого центра, то есть шесть величин, определяемых равенствами

(2.12)

(2.13)

Рекомендуемая литература – [7]:

Контрольные задания для СРС – изучить самостоятельно тему «Геометрическая и аналитическая форма задания сил»

Тема 3. Равновесие произвольной системы сил – 2 часа.

Дата добавления: 2014-01-07