Определение игры в нормальной форме

Предполагается, что игроки имеют возможность лишь один раз выбрать альтернативу (действие) из множества возможных действий. Также предполагается, что выбор действия игроки производят одновременно и независимо друг от друга, не зная выбора противников. После выбора всех действий реализуется определенный исход. Каждому исходу соответствуют значения полезности игроков, их выигрыши.

Всем игрокам известны как зависимость их выигрышей от исхода игры, так и выигрыши противников. То есть в таком виде определение игры в нормальной форме подходит только для игр с полной информированностью.

В соответствии с введенной выше классификацией, среди игр в нормальной форме можно выделить антагонuстuческuе игры, в которых сумма выигрышей игроков при любом исходе равна нулю, и игры с непротивоположными интересами, в которых сумма выигрышей может быть различной для разных ситуаций.

Для экономических задач и задач организационного управления типична ситуация, когда интересы игроков не противоположны. Тогда, в принципе, игроки могут быть заинтересованы в совместных действиях, например, в обмене информацией. Однако, иногда подобное кооперирование запрещено правилам и игры.

Определение 2 Игрой в нормальной форме п лиц с произвольной суммой называется система , где– непустые множества действий, 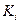– функции выигрыша игроков,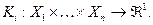

Обычно множества действий считаются компактами, то есть ограниченными замкнутыми множествами. Определения замкнутости и ограниченности подразумевают, что на множестве действий определено понятие сходимости, то есть задана, как минимум, топология. Часто в доказательствах необходимо наличие метрики на множестве действий. На практике множества действий игроков обычно представляют собой подмножества векторного пространства, для которых можно использовать евклидову метрику.

Если множества действий игроков конечны, то действия каждого игрока можно последовательно пронумеровать. Если, к тому же, игроков двое, выигрыши первого игрока можно представить в виде матрицы, в которой он выбирает действие – номер строки, его противник выбирает действие – номер столбца, а на пересечении столбца и строки находится число, соответствующее выигрышу первого игрока. Аналогичную матрицу можно построить и для второго игрока. Определенная с помощью пары таких матриц игра в нормальной форме называется биматричной.

Дата добавления: 2014-01-07