Регрессионная модель

Для описания, анализа и прогнозирования процессов в экономике применяют математические модели в форме каких-либо уравнений или функций.

Модель экономического объекта (или производственного процесса), отражая его основные свойства без учета второстепенных, позволяет судить об особенностях этого процесса в определенных конкретных условиях и прогнозировать его поведение в будущем.

Часто результирующий показатель 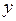является функций существенных и несущественных факторов:

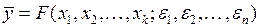(1)

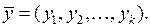
Существенные факторы 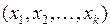– неслучайны, несущественные факторы 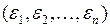случайны, но так как их много, пренебрегать ими нельзя.

Например, существенные факторы – труд, сырьё, оборудование, электроэнергия или их стоимость.

Несущественные факторы – влияние природных условий, ситуации на финансовом и фондовых рынках, политическая ситуация в регионе.

Уравнение (1) используется для малых промежутков времени и спокойного развития экономики.

Определение 1. Пусть задана функция 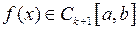,– k+1 непрерывно - дифференцируемая функция. Тогда в точке 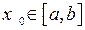справедлива формула Тейлора:

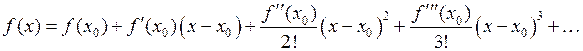
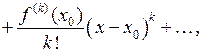где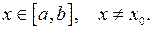

Для функции двух переменных ряд Тейлора имеет вид:

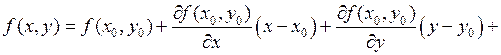
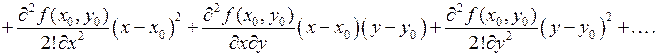Разложим (1) в ряд Тейлора в окрестности некоторой точки 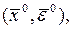где 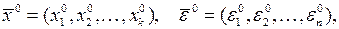мы получаем:

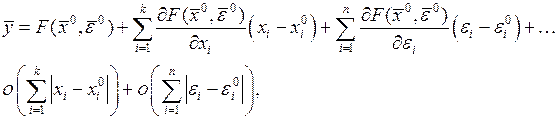(2)

где 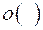– «о - малое».

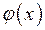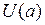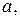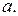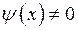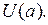Определение 2. Пусть даны две функции и заданные в некоторой окрестности точки за исключением, быть может, точки Будем считать, что на Если 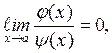то будем этот факт записывать так: 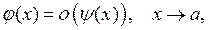и говорить, что 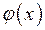есть о-малое от 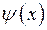при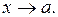

Например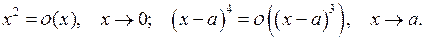

Обозначим в (2)

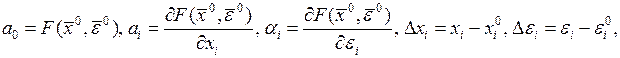
получаем:

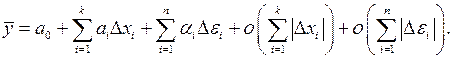(3)

В случае независимости случайных факторов, а также их относительно малого влияния на результат, если 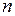велико, вся случайная составляющая 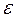распределена по нормальному закону (теорема Ляпунова). При этом если 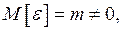то можно записать: 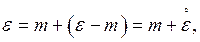где 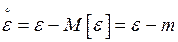– центрированная случайная величина (СВ). Найдем матожидание

Тогда присоединяя 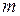к 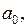получим 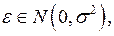т.е. 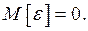Введем в (3) новые переменные 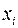вместо 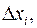окончательно приходим к следующей модели:

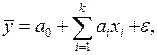(4)

где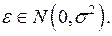

(4) – модель множественной линейной регрессии.

Если функция 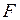в модели (1) зависит только от одного существенного фактора, то разлагая эту функцию в ряд Тейлора окрестности точки :

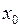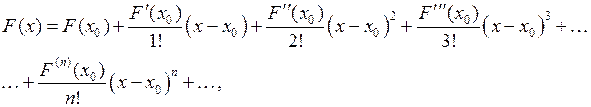
или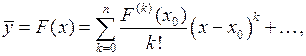

обозначим 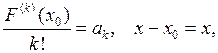получим:

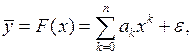(5)

где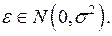

В равенствах (4), (5) первые слагаемые детерминированные (неслучайные), 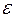- нормальная СВ, тогда 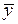также будет нормальной СВ, причем в (4): 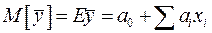− матожидание так как 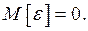В (5) 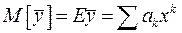− матожидание, - дисперсия, то есть

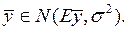
Классический метод наименьших квадратов

Модель (5) допускает следующую математическую интерпретацию. Пусть имеется некоторая зависимость фактора 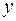от 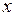. Измеряя эти факторы мы получим выборку:

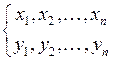(6)

Поскольку всякое измерение фактора 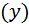имеет ошибку, то справедливо соотношение:

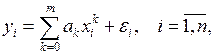(7)

где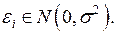

Как по выборке (6) найти коэффициенты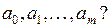

Для решения этой задачи применяют метод наименьших квадратов (МНК).

Предположим, что между независимой переменной 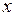и зависимой переменной) 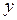имеется некая неизвестная функциональная связь 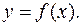Эта связь изображается выборкой (4) приближенных значений 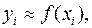полученных в ходе наблюдений или экспериментов. Требуется дать приближенное аналитическое описание этой связи. На практике удобно представить искомую зависимость в виде обобщенного многочлена:

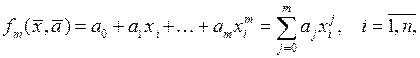(8)

(5)– многочлен степени,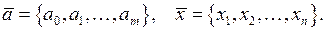Требуется найти такие коэффициенты 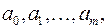чтобы минимизировать сумму квадратов отклонении эмпирических значений функции 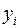от теоретических значений 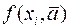в тех же точках, т.е. решаем задачу:

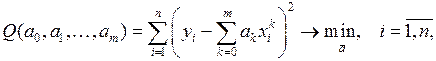
т.е. найти такие коэффициенты, которые доставляют минимум функции 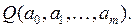Получаем задачу нахождение минимума функции многих переменных.

Запишем необходимое условие экстремума функции:

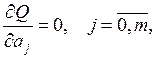получим:

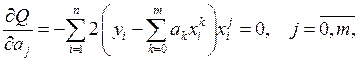
или, раскрывая скобки:

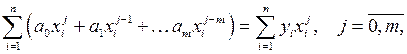
делая преобразования, получим:

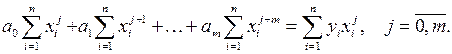(9)

Уравнение (9) представляет собой СЛАУ, так как неизвестные 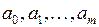входят в них линейно. Система состоит из 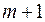уравнений и содержит 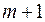неизвестное. Можно показать, что при 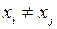определитель СЛАУ отличен от нуля. Следовательно (9) имеет единственное решение и в этой точке функция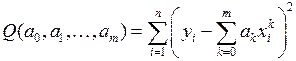

достигает минимума.

Учитывая, что при 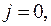запишем СЛАУ (9) в следующем виде при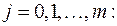

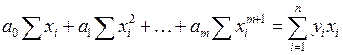. (10)

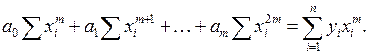
Обозначим: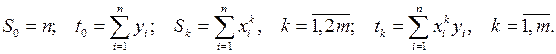

Тогда (10) преобразуется к виду:

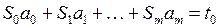
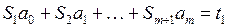(11)

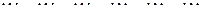
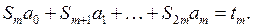
Решая СЛАУ (11) методом Гаусса или Крамера, получаем

Пример 1. Предположим, что между независимой переменной 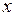и зависимой переменной 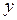имеется некая неизвестная функциональная связь 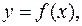заданная таблицей (табл. 1). Решить задачу МНК для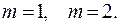

Таблица 1

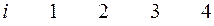
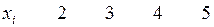
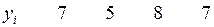
Решение:

1). Пусть степень многочлена 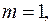тогда решение ищется в виде: 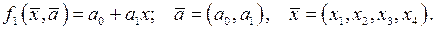Составим систему (9):

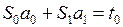
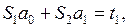
где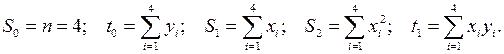

В результате получаем (табл. 2):

Таблица 2

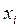
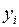
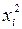
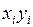
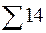
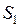
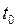
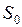
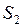
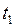
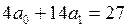
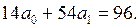
Исключая первое неизвестное, получим:

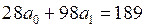
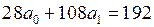
Искомая сглаживающая функция: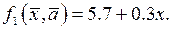

2). Пусть тогда решение ищется в виде: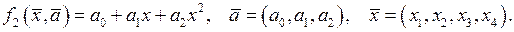

Составим систему (9):

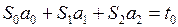
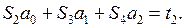
Таблица 3

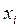
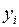
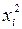
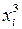
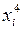
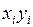
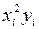
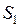
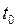
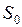
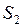
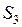
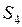
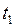
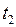
В результате (табл.3) получаем систему:

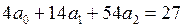
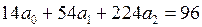
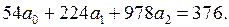
Решая систему методом Гаусса, получим: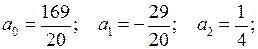

искомая сглаживающая функция: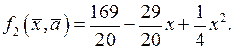

Пример 2. Предположим, что между независимой переменной 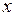и зависимой переменной 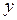имеется некая неизвестная функциональная связь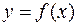заданная таблицей (табл. 4). Решить задачу МНК для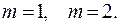

Таблица 4

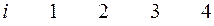
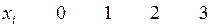
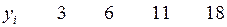
Пример 3. Предположим, что между независимой переменной 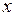и зависимой переменной 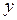имеется некая неизвестная функциональная связь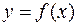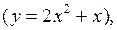заданная таблицей (табл. 5). Решить задачу МНК для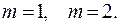

Таблица 5

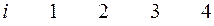
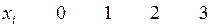
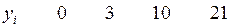
Пример 4. Предположим, что между независимой переменной 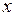и зависимой переменной 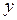имеется некая неизвестная функциональная связь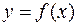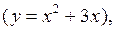заданная таблицей (табл. 6). Решить задачу МНК для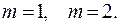

Таблица 6

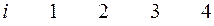
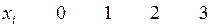
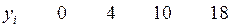
Пример 5. Предположим, что между независимой переменной 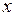и зависимой переменной 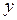имеется некая неизвестная функциональная связь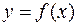заданная таблицей (табл. 6). Решить задачу МНК для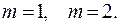

Таблица 6

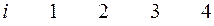
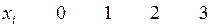
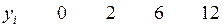
Пример 6. Предположим, что между независимой переменной 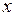и зависимой переменной 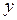имеется некая неизвестная функциональная связь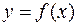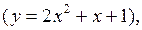заданная таблицей (табл. 7). Решить задачу МНК для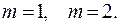

Таблица 7

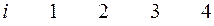
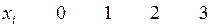
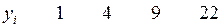
Пример 6. Предположим, что между независимой переменной 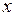и зависимой переменной 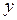имеется некая неизвестная функциональная связь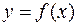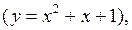заданная таблицей (табл. 8). Решить задачу МНК для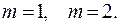

Таблица 8

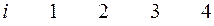
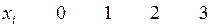
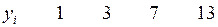
Дата добавления: 2014-01-07