Конические зубчатые передачи

Передают вращающий момент между валами с пересекающимися осями (чаще всего под углом 90⁰). Их зубья бывают прямыми, косыми, круговыми и обычно имеют эвольвентный профиль.

И хотя, конические колёса сложнее цилиндрических как по своей геометрии, так и в изготовлении, принципы силового взаимодействия, условия работы, а следовательно, и методика расчёта аналогичны цилиндрическим.

Здесь мы рассмотрим только отличительные особенности расчёта конических колёс.

Сначала конструктор выбирает внешний окружной модуль m_te, из которого рассчитывается вся геометрия зацепления, в частности, нормальный модуль в середине зуба m_nm= m_te (1 – 0,5 b/R_e ),

где R_e – внешнее конусное расстояние.

Силы в конической передаче действуют аналогично цилиндрической, однако следует помнить, что из-за перпендикулярности осей радиальная сила на шестерне аналогична осевой силе для колеса и наоборот, а окружная сила при переходе от шестерни к колесу только меняет знак

; .

Прочностные расчёты конических колёс [45] проводят аналогично цилиндрическим, по той же методике [3]. Из условия контактной выносливости определяют внешний делительный диаметр d_we, из условия прочности на изгиб находят нормальный модуль в середине зуба m_nm. При этом в расчёт принимаются воображаемые эквивалентные колёса с числами зубьев Z_э1,2 =Z_1,2 / cosd_1,2 и диаметры d_э1,2 = m_te Z_1,2 / cosd_1,2. Здесь Z₁, Z₂, - фактические числа зубьев конических колёс. При этом числа Z_э1,2 могут быть дробными.

В эквивалентных цилиндрических колёсах [32] диаметр начальной окружности и модуль соответствуют среднему сечению конического зуба, вместо межосевого расстояния берётся среднее конусное расстояние [45], а профили эквивалентных зубьев получают развёрткой дополнительного конуса на плоскость.

7.1 Расчёт закрытой конической зубчатой передачи

Рис.2.4

Наибольшее применение в редукторостроении получили прямозубые конические колёса, у которых оси валов пересекаются под углом =90 (рис. 2.4).

Проектный расчёт. Основной габаритный размер передачи - делительный диаметр колеса по внешнему торцу - рассчитывают по формуле [1]:

,

где Епр - приведённый модуль упругости, для стальных колёс Епр =Естали= =2,1105 МПа;

T2 - вращающий момент на валу колеса, Нмм (см.п.2.3);

KH - коэффициент неравномерности распределения нагрузки по длине зуба, определяют по графикам на рис. 2.5.

Здесь Кbe - коэффициент ширины зубчатого венца относительно внешнего конусного расстояния, . Рекомендуют принять Кbe 0,3. Меньшие значения назначают для неприрабатываемых зубчатых колёс, когда H1 и H2 > 350 HB или V > 15 м/с.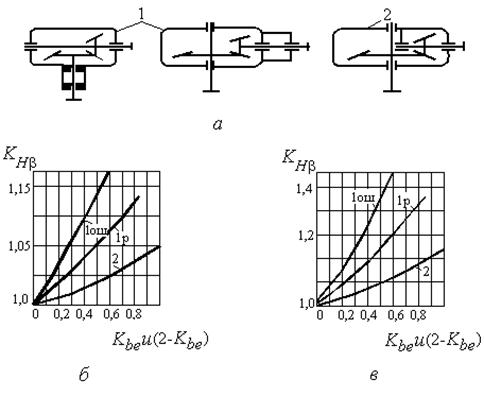

Рис. 2.5

Наиболее распространено в редукторостроении значение Кbe = 0,285, тогда предыдущее выражение для определения делительного диаметра по внешнему торцу колеса принимает вид

,

где up – расчетное передаточное число конической передачи.

Геометрический расчёт. Определяют диаметр шестерни по внешнему торцу .

Число зубьев шестерни назначают по рекомендациям, представленным на рис. 2.6.

По значению определяют число зубьев шестерни:

при Н1 и Н2 350 HB,

при Н1 45 HRC и Н2 350 HB,

при Н1 и Н2 45 HRC.

Вычисленное значение z1 округляют до целого числа.

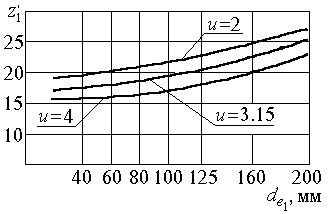
Рис.2.6

Определяют число зубьев колеса .

Вычисленное значение округляют до целого числа. После этого необходимо уточнить:

- передаточное число передачи ,

- угол делительного конуса колеса ,

- угол делительного конуса шестерни ,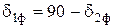

- внешний окружной модуль .

Рекомендуется округлить до стандартного значения по ряду модулей: 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10. После этого уточняют величины диаметров и .

Рассчитывают величину внешнего конусного расстояния передачи (рис.2.4) .

Рабочая ширина зубчатого венца колеса .

Полученное значение округляют до ближайшего из ряда нормальных линейных размеров (табл. 2.5).

Определяют расчётный модуль зацепления в среднем сечении зуба

.

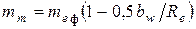При этом найденное значение не округляют!

Рассчитывают внешнюю высоту головки зуба .

Внешнюю высоту ножки зуба определяют как .

Внешний диаметр вершин зубьев колёс рассчитывают по формуле

.

Угол ножки зуба рассчитывают по формуле .

Проверочный расчёт. При расчёте на выносливость зубьев колёс по контактным напряжениям проверяют выполнение условия

,

где Eпр -приведённый модуль упругости, для стальных колёс Eпр = Eстали = =2,1105 МПа;

- вращающий момент на шестерне, Нмм, ;

здесь - кпд передачи.

- коэффициент расчётной нагрузки, ; коэффициент концентрации нагрузки найден ранее по графикам рис.2.5.

- коэффициент динамической нагрузки, находят по табл. 2.7 с понижением на одну степень точности против фактической, назначенной по окружной скорости в соответствии с рекомендациями (табл.2.6);

- делительный диаметр шестерни в среднем сечении зуба,

;

- угол зацепления, =20.

Далее проверяют зубья колёс на выносливость по напряжениям изгиба по формулам [1]:

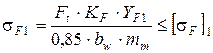и ,

где - окружное усилие в зацеплении, Н, ;

- коэффициент расчётной нагрузки, . Здесь , а определяют по табл. 2.7 с понижением точности на одну степень против фактической.

- коэффициент формы зуба соответственно шестерни и колеса, находят по табл. 2.9 в зависимости от эквивалентного числа зубьев колёс

.

7.2 Проектный расчёт открытой конической прямозубой передачи

Модуль зацепления в среднем сечении зуба конического колеса рассчитывают по формуле

,

где, кроме рассмотренных выше величин (см. п. 2.6), рекомендуют назначить и =1,1…1,2.

Далее рассчитывают основные геометрические параметры зубчатых колёс открытой передачи:

- ширину зубчатого венца (с округлением до целого числа по ряду нормальных линейных размеров);

- делительный диаметр в среднем сечении зуба шестерни ;

- по заданному (или принятому) передаточному числу uотк находим угол при вершине делительного конуса ;

- среднее конусное расстояние ;

- внешнее конусное расстояние ;

- модуль зацепления на внешнем торце ;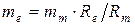

- внешний делительный диаметр шестерни .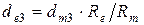

Проверочный расчет такой передачи на выносливость по контактным напряжениям выполняют в соответствии с п.2.7 («Расчет закрытой конической зубчатой передачи»).

8 ЧЕРВЯЧНЫЕ ПЕРЕДАЧИ

Червячная передача имеет перекрещивающиеся оси валов, обычно под углом 90°. Она состоит из червяка – винта с трапецеидальной резьбой и зубчатого червячного колеса с зубьями соответствующей специфической формы.

Движение в червячной передаче преобразуется по принцпу винтовой пары. Изобретателем червячных передач считают Архимеда.

Достоинства червячных передач:

+ большое передаточное отношение (до 80);

+ плавность и бесшумность хода.

В отличие от эвольвентных зацеплений, где преобладает контактное качение, виток червяка скользит по зубу колеса. Следовательно, червячные передачи имеют "по определению" один фундаментальный недостаток: высокое трение в зацеплении. Это ведёт к низкому КПД (на 20-30% ниже, чем у зубчатых), износу, нагреву и необходимости применять дорогие антифрикционные материалы.

Кроме того, помимо достоинств и недостатков, червячные передачи имеют важное свойство: движение передаётся только от червяка к колесу, а не наоборот. Никакой вращающий момент, приложенный к колесу, не заставит вращаться червяк. Именно поэтому червячные передачи находят применение в подъёмных механизмах, например в лифтах. Там электродвигатель соединён с червяком, а трос пассажирской кабины намотан на вал червячного колеса во избежание самопроизвольного опускания или падения.

Это свойство не надо путать с реверсивностью механизма. Ведь направление вращения червяка может быть любым, приводя либо к подъёму, либо к спуску той же лифтовой кабины.

Передаточное отношение червячной передачи находят аналогично цилиндрической U = n₁ / n₂ = Z₂ / Z₁.

Здесь Z₂ – число зубьев колеса, а роль числа зубьев шестерни Z₁ выполняет число заходов червяка, которое обычно бывает равно 1, 2, 3 или 4.

Очевидно, что однозаходный червяк даёт наибольшее передаточное отношение, однако наивысший КПД достигается при многозаходных червяках, что связано с уменьшением трения за счёт роста угла трения.

Основные причины выхода из строя червячных передач:

r поверхностное выкрашивание и схватывание;

r излом зуба.

Это напоминает характерные дефекты зубчатых передач, поэтому и расчёты проводятся аналогично [44].

В осевом сечении червячная пара фактически представляет собой прямобочное реечное зацепление, где радиус кривизны боковой поверхности "рейки" (винта червяка) r₁ равен бесконечности и, следовательно, приведённый радиус кривизны равен радиусу кривизны зуба колеса

r_пр = r₂.

Далее расчёт проводится по формуле Герца-Беляева. Из проектировочного расчёта находят осевой модуль червяка, а по нему и все геометрические параметры зацепления.

Особенность расчёта на изгиб состоит в том, что принимается эквивалентное число зубьев Z_экв = Z₂ / cos³g, где g - угол подъёма витков червяка.

Вследствие нагрева, вызванного трением, червячные передачи нуждаются также и в тепловом расчёте. Практика показывает, что механизм опасно нагревать выше 95^оС. Допускаемая температура назначается 65 ^oC.

Уравнение для теплового расчёта составляется из баланса тепловой энергии, а именно: выделяемое червячной парой тепло должно полностью отводиться в окружающую среду

Q_{выделяемое} = Q_{отводимое}.

Решая это уравнение, находим температуру редуктора, передающего заданную мощность N

t = [ 860 N (1- η )] / [ K_T S (1- Ψ )] + t_o.

где K_T – коэффициент теплоотдачи, S – поверхность охлаждения (корпус), t_o – температура окружающей среды, Y – коэффициент теплоотвода в пол.

В случае, когда расчётная температура превышает допускаемую, то следует предусмотреть отвод избыточной теплоты. Это достигается оребрением редуктора, искусственной вентиляцией, змеевиками с охлаждающей жидкостью в масляной ванне и т.д.

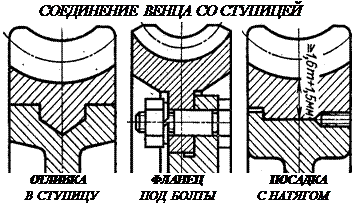
Оптимальная пара трения это "сталь по бронзе". Поэтому при стальном червяке червячные колёса должны выполняться из бронзовых сплавов. Однако цветные металлы дороги и поэтому из бронзы выполняется лишь зубчатый венец, который крепится на сравнительно дешёвой стальной ступице. Таким образом, червячное колесо - сборочная единица, где самые популярные способы крепления венца это либо центробежное литьё в кольцевую канавку ступицы; либо крепление венца к ступице болтами за фланец; либо посадка с натягом и стопорение винтами для предотвращения взаимного смещения венца и ступицы.

Крепление венца к ступице должно обеспечивать фиксацию как от проворота (осевая сила червяка = окружной силе колеса), так и от осевого "снятия" венца (окружная сила червяка = осевой силе колеса).

КОНТРОЛЬНЫЕ ВОПРОСЫ

s Каково назначение передач в машинах?

s Каковы области применения прямозубых и косозубых передач?

s Каковы сравнительные достоинства прямозубых и косозубых колёс?

s Как определяется передаточное отношение и передаточное число?

s Каковы главные виды разрушений зубчатых колёс?

s Какие силы действуют в зубчатом зацеплении?

s Какие допущения принимаются при расчёте зубьев на контактную прочность?

s По какой расчётной схеме выполняется расчёт зубьев на изгиб?

s В чём заключаются достоинства и недостатки планетарных передач?

s Для чего созданы волновые передачи и в чём заключается принцип их работы?

s В чём заключаются достоинства и недостатки волновых передач?

s Для чего созданы зацепления Новикова и в чём заключается принцип конструкции их зубьев?

s В чём заключаются достоинства и недостатки зацеплений Новикова?

s В чём заключается принцип конструкции червячной передачи?

s Каковы достоинства и недостатки червячных передач?

s Какое свойство червячной передачи отличает её от других передач?

s Каковы основные причины поломок червячных передач?

s Из каких условий находят температуру червячной передачи?

s Какие методы могут применяться для снижения температуры червячной передачи?

s Какие материалы должны применяться для червячной передачи?

s Каковы особенности конструкции червячных колёс?

Дата добавления: 2014-01-07