Требования к оценкам измеряемой величины

О выборе количества измерений

Обработка результатов измерений

При увеличении числа независимых измерений n оценка некоторой величины должна сходиться по вероятности к математическому ожиданию случайной величины, тогда такая оценка будет называться состоятельной.

Пусть произведено n независимых измерений случайной величины X с результатами X₁, Х₂,...X_n. Для оценки действительного значения измеряемой величины используется, как указывалось выше, среднее арифметическое значение m_x^*, являющееся оценкой математического ожидания данной величины m_x, т.е.

m_x^*=

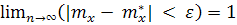
D_x^*=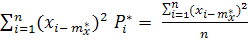

(17)

где - статистическая вероятность значения X.

Покажем, что оценка дисперсии (17) является состоятельной.

D_x^*= - 2=

(18)

Первый член в формуле (18) представляет среднее арифметическое n измеренных значений величины X и при неограниченном увеличении числа измерений сходится по вероятности к начальному моменту второго порядка а₂ [X] = М[ X²]. Второй член сходится по вероятности к величине m_х² [X] = (М [Х])². Следовательно, вся величина (18) по вероятности сходится к величине

D_x= α₂[X] – m_x2,

(19)

что доказывает состоятельность оценки (17), т.к. соотношение (19) является теоретическим определением дисперсии случайной величины.

Одним из условий получения надежных оценок является требование их несмещенности, которое заключается в том, чтобы при замене оценкой m_x^* действительного значения Х_д не допускалась систематическая погрешность. Это требование приводит к необходимости выполнения следующего условия: математическое ожидание оценки должно при любом числе измерений совпадать с действительным значением величины, т.е.

M [m_x^*] = X_д

(20)

Оценка m_x^* является несмещенной, так как

M [m_x^*] =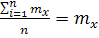

Для статистической дисперсии D_х* известно соотношение

M [D_x^*] = ,

(21)

из которого следует, что, заменяя дисперсию D_x ее оценкой D_x *, допускаем систематическую погрешность тем большую, чем меньше число n измерений. Следовательно, для исключения этой систематической погрешности необходимо видоизменять запись для оценки дисперсии:

Поэтому несмещенной оценкой дисперсии D_х является величина

D_x^* =

(22)

Если выбранная несмещенная оценка по сравнению с другими возможными оценками имеет наименьшую дисперсию, то такая оценка является эффективной, например, D[m_x] = min

Дата добавления: 2014-01-07