Идентификация законов распределения величин по результатам измерений

На практике измерений знание реального закона распределения измеряемых величин необходимо для получения достоверных результатов измерений. После проведения соответствующей серии измерений строится эмпирический закон распределения измеряемой величины и нужно сопоставить ему модель теоретического закона распределения, т.е. идентифицировать неизвестный нам закон распределения возможных значений измеряемой величины. Эта задача решается с помощью широко применяемых в математической статистике критериев согласия. Среди известных критериев согласия наиболее применяемым является критерий согласия хи - квадрат (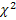). Основные принципы его использования следующие.

Пусть произведено n независимых измерений некоторой величины X, рассматриваемой как случайной. Результаты измерений обычно представляют в виде вариационного ряда, т.е. в виде последовательности измеренных значений величины, расположенных в порядке возрастания от наименьшего к наибольшему. Например, путь имеются результаты измерений постоянного электрического напряжения U, приведенные в табл.2.

Таблица 2

Номер измерения

U, В

Данные, приведенные в табл. 2, преобразуем в вариационный рад, записанный в табл. 3.

Таблица 3

Номер ряда

U, B

Далее весь диапазон измеренных значений величины U разделяется на некоторое число разрядов k (интервалов). Число этих разрядов определяется в соответствии с соотношением:

k= 3 ∙ lgn + 1 (28)

где n - число измерений.

В нашем случае имеем

k= 3∙ lg20 + 1 ≈ 4.9.

Определяем значение до ближайшего целого и получаем, что k = 5.

После определения числа разрядов вариационного ряда строится статистический ряд- таблица, в которой приведены длины разрядов Ii (в порядке их соответствия оси абсцисс измеряемой величины U), количества значений величины m_i, оказавшихся в том или ином разряде, а также статистические частоты Pi^*. Для нашего примера эти данные сведены в табл.4. Очевидно, что

ΣP_i^* = 1 Р_i^*= m_i / n

Таблица 4

Ii	47.5-48.5	48.5 - 49.5	49.5 - 50.5	50.5-51.5	51.5-52.5
Mi
Рi^*	0.1	0.25	0.2	0.3	0.15

Если принять, что теоретический закон нормальный, то с помощью формулы (27) можно определить теоретическую вероятность в каждом соответствующем разряде (U_i, U_i+1), т.е.

P_i = Ф() - Ф()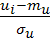

(29)

где m_u и σ_u - соответственно, математическое ожидание и СКО величины U.

Поскольку m_u и σ_u неизвестны, при расчетах их заменяют статистическими значениями m_u * - средним арифметическим значением и статистическим СКО σ_u *. Среднее арифметическое значение погрешности m_u * найдем по формуле:

m_u^* =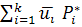

где 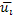- среднее арифметическое значение U в i-ом разряде.

Для приведенного примера имеем:

m_u* = (48 • 0.1) + (49 • 0.25) +(50 • 0.2) + (51 • 0.3)+ (52 • 0.15) = 50.15.

Статистическую дисперсию определим с помощью формулы:

σ_u^*2=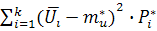

Тогда σ_u^*2 = (48 - 50.15)² • 0.1 + (49-50.15)² • 0.25 + (50 - 50.15)² • 0.2 + (51 - 50.15)² • 0.3 + (52 - 50.15)² • 0.15 = 1.52

Соответственно, σ_u^* = 1.23.

Далее находим теоретические вероятности попадания случайной величины в каждый из разрядов, используя формулу (29) и таблицу функции Лапласа, т.е.

Р1 = Ф ((48.5 - 50.15) / 1.23) - Ф ((47.5 - 50.15) /1.23) = 0.07.

Поступая аналогично, получим

Р2 = 0.21; Р3=0.31; Р4 = 0.24; Р5 = 0.12.

Обратим внимание, что сумма всех теоретических вероятностей равна 0.95, а должна быть равна 1. Это расхождение связано с тем, что из таблицы функций Лапласа мы брали значения с точностью до второго знака после запятой, а для получения в сумме 1 необходимо было брать значения функции Лапласа с более высокой точностью, например, до четвертого знака после запятой. В качестве меры расхождения между теоретическими вероятностями и статистическими частотами критерий хи - квадрат предусматривает использование величины:

χ² = n (30)

где n и k - число измерений и число разрядов статистического ряда, соответственно.

В теории математической статистики доказано, что при большом числе измерений n закон распределения величины χ ² практически не зависит от вида функции распределения F(х) изучаемой величины, а зависит только от числа разрядов k(n). При неограниченном увеличении числа n этот закон близок к распределению хи-квадрат с r степенями свободы (это есть распределение суммы квадратов г независимых случайных величин, каждая из которых распределена по нормальному закону с математическими ожиданиями, равными нулю, и дисперсией, равной единице), с плотностью распределения величины U= χ²

ƒ _χ2(u) = 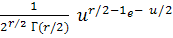, при u>0,

где 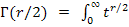e^-tdt - гамма- функция.

Число степеней свободы распределения хи-квадрат г = k - s, где s - число независимых условий, которым должны удовлетворять статистические вероятности Р_i². Число s определяется формой теоретического закона распределения. Для симметричных законов распределения, каковым является и нормальный закон, таких независимых условий три:

1. Сумма статистических вероятностей должна быть равной единице, т.е.

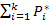= 1

2. Математическое ожидание m_u и среднее арифметическое значение m_u* должны совпадать, т.е.

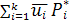m_u = = m_u*

3. Теоретическая и статистическая дисперсии должны совпадать, т.е.

σ_u²= 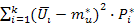= σ_u^*2

Таким образом, используя формулу (30) с учетом, что в нашем случае k = 5; n = 20, находим χ², т.е.

χ² = 20[ +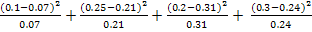

Находим число степеней свободы r для нашего случая: r = k - s = 5 - 3 =2.

Берем математические таблицы для значений χ²зависимости от r = 2 и от вероятности сходимости эмпирического и теоретического законов распространения и для значения χ^{2 =} 0.64 получим, что эта вероятность равна 0.75 (указанные таблицы имеются в любом учебнике по математической статистике).

Вероятность p = 0.75 следует считать вполне достаточной для того, чтобы сделать вывод о том, что гипотеза о соответствии эмпирического закона нормальному закону распределения не противоречит полученным экспериментальным данным.

Обратим внимание на высказанное выше суждение. Здесь не говорится о том, что полученные экспериментальные данные соответствуют нормальному закону. Этого утверждать в рамках применяемых методов математической статистики мы не можем. Мы только утверждаем, что гипотеза о возможности соответствия экспериментальных данных нормальному закону в рамках критерия хи-квадрат выполняется с вероятностью 0.75.

Как отмечалось выше, возможно применение и других критериев согласия, известных в математической статистике, но критерий хи-квадрат является наиболее широко используемым.

Дата добавления: 2014-01-07