Понятия и определения

Лекция 1

Механика – это раздел физики изучающий механическое движение как процесс изменения взаимного расположения тел или их частей в пространстве с течением времени.

Механика при ее изучении разделяется на две части: кинематика и динамика.

Кинематика изучает механическое движение без учета причин, а динамика с учетом сил действующих на тело.

В кинематике тело рассматривается как материальная точка (м.т.), которая является моделью макроскопического тела, размерами которого можно пренебречь в условиях данной задачи.

1.1.1. Система отсчета

Движение материальной точки (м.т.) всегда рассматривается относительно какого-либо другого тела, которое принимается за неподвижное.

Тело, которое считается неподвижным и по отношению к которому определяется положение других тел, называется, телом отсчета.

Положение м.т. в пространстве определяется с помощью системы координат X,Y,Z, связанной с телом отсчета.

Совокупность тела отсчета, жестко связанной с ним системы координат и часов, образует систему отсчета.

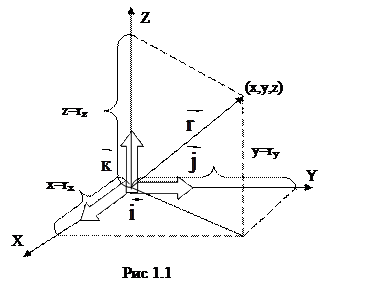Положение материальной точки в декартовой системе координат определяется через ее координаты x, y, z или радиус-вектор 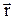, проведенный в заданную точку из начала координат (рис 1.1). Радиус-вектор 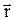и его проекции на оси координат определяется из соотношений:

,

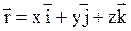(1.1)

где 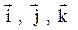– единичные векторы осей координат.

Модуль вектора

. (1.2)

1.1.2. Траектория, путь, перемещение

При движении м.т. относительно выбранной системы отсчета ее радиус-вектор и его координаты зависят от времени.

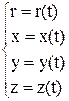(1.3)

Совокупность всех последовательных положений материальной точки в пространстве определяет траекторию ее движения. Уравнение траектории z=z (x,y) находится в результате решения системы уравнений (1.3 ) путем исключения параметра t.

Движение называется прямолинейным, если его траектория – прямая линия, и криволинейным во всех других случаях. Вид траектории не зависит от выбора системы отсчета, а ее кривизна

τ₂    

τ₂  

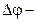где угол между касательным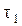и и , проведенными в точках 1 и 2 (рис. 1.2), - длина участка траектории. Величина, обратная кривизне С, называется радиусом кривизны

.

При движении м.т. по произвольной криволинейной траектории в выбранной системе отсчета, за интервал времени 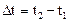радиус-вектор изменяется на 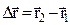. Вектор 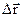называется вектором перемещения (рис 1.3).

За интервал времени 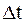м.т. проходит участок траектории . Длина этого участка обозначается через s и называется путь. Путь может быть больше модуля вектора перемещения или равен ему. Равенство наблюдается только в частных случаях – при прямолинейном движении тела в одном направлении, и для бесконечно малых промежутков времени .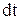

1.1.3. Скорость

Скорость — это векторная величина, характеризующая быстроту изменения положения м.т. в пространстве.

Для характеристики движения м.т. вводят понятие средней и мгновенной скорости.

Средней скоростью называется вектор, равный отношению вектора перемещения 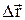к промежутку времени 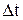, в течение которого произошло перемещение м.т.

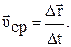
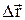Направление , совпадает с направлением вектора перемещения , () (рис 1.3)

Мгновенной скоростью называется предельное значение вектора средней скорости при стремлении 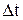к нулю

(1.4)

Вектор перемещения направлен по секущей и при стремлении 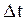к нулю стремится к касательной в точке 1 (рис. 1.4).

Следовательно, вектор мгновенной скорости 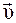направлен по касательной в заданной точке траектории в сторону движения м.т.

Модульмгновенной скорости определяется из соотношения

, (1.5)

Путь, пройденный материальной точкой за интервал времени от t₁ до t₂

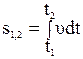, (1.6)

где , называется путевой скоростью.

С учетом соотношений (1.1)

(1.7)

где – проекции скорости точки на оси координат.

Модуль вектора скорости в декартовой системе координат

. (1.8)

1.1.4. Ускорение

В процессе движения направление и модуль вектора скорости м.т. могут изменяться. Изменение вектора скорости определяется ускорением.

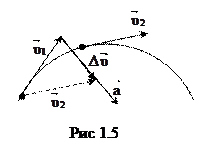Ускорение материальной точки — векторная величина, характеризующая быстроту изменения вектора скорости с течением времени.

По аналогии со средней и мгновенной скоростью вводят понятие среднего и мгновенного ускорения. Пусть в момент времени t₁ м.т. имеет скорость , а в момент t₂ – скорость (рис. 1.5). Тогда за промежуток времени вектор скорости изменится на величину 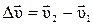, а среднее ускорение

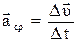. (1.9)

Вектор 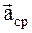, совпадает с вектором .

Мгновенное ускорение

(1.10)

где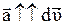

С учетом соотношений (1.1) и (1.7)

, (1.11)

где – проекции ускорения точки на оси координат.

Дата добавления: 2014-01-07