
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тема 5. Средние величины
|
|
|
|
5.1. Понятие и виды средних величин
5.2. Использование метода моментов для определения средней величины
5.3. Структурные средние величины (мода и медиана)
5.1. Наиболее распространенной формой статистических показателей, используемой в экономических исследованиях, является средняя величина. Средней величиной называется значение признака, наиболее характерное для изучаемой совокупности.
Важным свойством средней величины является ее способность отражать то общее, что присуще всем единицам исследуемой совокупности. Значение признака в совокупности изменяется под действием множества разнообразных факторов, среди которых могут быть как основные, так и случайные. Сущность средней заключается в том, что в ней погашаются отклонения значений признака, обусловленные действием случайных факторов, и учитываются изменения, вызванные действием основных факторов. Это позволяет средней величине отражать типичное значение признака и абстрагироваться от индивидуальных особенностей, присущих отдельным единицам совокупности. Объективность и типичность средней величины обеспечивается при следующих условиях:
1) средняя величина должна рассчитываться по массовым данным;
2) средняя величина должна рассчитываться для качественно однородной совокупности, т.е. расчет средней должен сочетаться с методом группировок.
В экономических исследованиях и расчетах применяют две категории средних величин:
1) степенные средние (средняя арифметическая, средняя гармоническая, средняя геометрическая, средняя квадратическая);
2) структурные средние (мода и медиана).
Степенные средние могут быть простыми и взвешенными.
Основные расчетные формулы степенных средних величин представлены в табл. 5.1.
Таблица 5.1
Основные расчетные формулы степенных средних
| Средняя | Простая | Взвешенная | Условные обозначения |
| Степенная | 
| 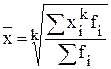
| 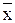 - средняя величина изучаемого признака; - средняя величина изучаемого признака;
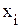 - i-тое значение изучаемого признака;
n - число различных значений изучаемого признака; - i-тое значение изучаемого признака;
n - число различных значений изучаемого признака;
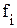 - частота (вес) i-го значения изучаемого признака. - частота (вес) i-го значения изучаемого признака.
|
1. Арифметическая 
| 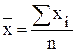
| 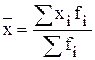
| |
2. Гармоническая 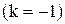
| 
| 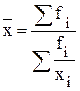
| |
3. Геометрическая 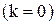
| 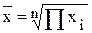
| 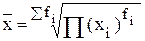
| |
4. Квадратическая 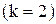
| 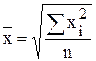
| 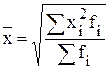
|
Использование средней арифметической простой и взвешенной и средней гармонической простой и взвешенной рассмотрим на следующих примерах.
Пример 5.1. Имеются данные о выработке шести рабочих цеха за смену.
| Табельный номер рабочего | Выработка, шт./час |
Необходимо определить среднюю выработку рабочего.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 263; Нарушение авторских прав?; Мы поможем в написании вашей работы!