Тема 6. Вариационный анализ

6.1. Показатели вариации и способы их расчета

6.2. Виды дисперсий. Правило сложения дисперсий

6.1. Вариацией называется изменение значения признака в пределах изучаемой совокупности. Для осуществления вариационного анализа рассчитываются следующие основные показатели вариации: размах вариации, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение и коэффициент вариации.

Размах вариации представляет собой максимальное значение, на которое изменяется варьирующий признак в совокупности и определяется по формуле:

,

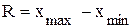где 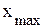, 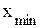- соответственно максимальное и минимальное значения признака.

Среднее линейное отклонение − это среднее арифметическое модуля отклонения каждого значения признака от его средней величины. Определяется:

- для совокупности:

;

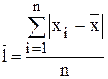- для ряда распределения:

,

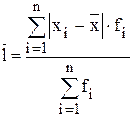где 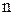- количество значений признака (интервалов);

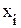- i-тое значение признака (середины интервала);

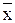- среднее значение признака;

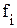- частота i-го значения признака (интервала).

Дисперсия − это среднее арифметическое квадрата отклонения каждого значения признака от его средней величины. Определяется:

- для совокупности:

;

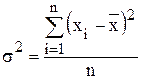- для ряда распределения:

.

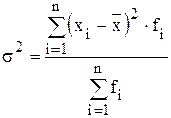Дисперсии присущи следующие математические свойства:

1) уменьшение или увеличение каждого значения изучаемого признака на одну и туже величину не приводит к изменению дисперсии:

;

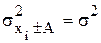2) уменьшение или увеличение каждого значения изучаемого признака в А раз приводит к изменению дисперсии в А² раз:

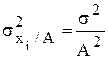или ;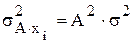

3) уменьшение или увеличение частоты каждого значения изучаемого признака в одно и тоже число раз не приводит к изменению дисперсии:

;

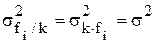4) дисперсия, вычисленная от средней арифметической, всегда меньше дисперсии, вычисленной от любой другой величины, на квадрат разности между средней и этой величиной:

.

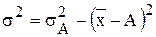Приняв 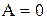, дисперсию ряда распределения можно рассчитать как разность между средним квадратом значения признака и квадратом среднего значения признака:

,

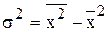где 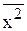- средний квадрат значения признака, рассчитывается:

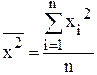или ;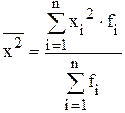

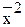- квадрат среднего значения признака.

Для расчета дисперсии часто используется метод моментов (метод отсчета от условного нуля), в основе которого лежат математические свойства дисперсии.

Согласно методу моментов дисперсия рассчитывается по формуле:

,

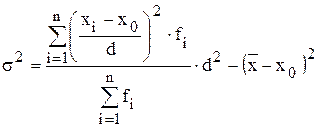где 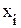- i-тое значение признака или середина i-го интервала;

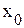- значение признака (середина интервала), имеющего наибольшую частоту (условный нуль);

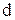- общий множитель для всех значений признака или их отклонений от условного нуля (для ряда с равными интервалами принимается длина интервала);

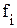- частота i-го значения признака или частное от его сокращения на наибольший общий делитель .

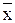- среднее значение признака, рассчитанное по методу моментов.

Пример 6.1. По данным о выпуске продукции предприятиями отрасли (столбцы 1 и 2 таблицы) определить по методу моментов дисперсию ряда.

Дата добавления: 2014-01-07