Тема 9. Метод выборочного наблюдения

Статистика имеет дело с массовыми совокупностями, статистические исследования которых весьма трудоемки и дорогостоящи. Поэтому сплошное наблюдение по возможности заменяется выборочным − наиболее совершенным и научно обоснованным способом несплошного наблюдения.

Выборочное наблюдение − это способ наблюдения, при котором обследуется не вся генеральная совокупность, а лишь ее часть, сформированная по определенным правилам, а полученные результаты характеризуют всю генеральную совокупность.

Несплошному наблюдению свойственны ошибки репрезентативности. Репрезентативность − это способность выборочной совокупности представлять генеральную совокупность.

В выборочном наблюдении решаются две основные задачи:

- определение с заданной вероятностью предельной ошибки выборки;

- нахождение объема выборки, необходимого для получения результатов с заданной степенью точности.

Для решения этих задач используют следующее соотношение:

,

где 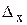- предельная ошибка выборки;

- дисперсия выборочной совокупности;

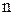- объем выборки;

- коэффициент доверия.

Значение коэффициента доверия зависит от величины вероятности, с которой необходимо получить результат. Значения коэффициента доверия для разных вероятностей определяются на основе использования интеграла вероятностей Лапласа и представлены в специально сформированной таблице. Например, если результат необходимо получить с вероятностью значение 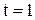, для вероятности 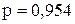значение 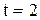, а для вероятности значение 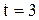и т.д.

Приведенная формула позволяет определить предельную ошибку выборки, сформированной повторным способом отбора, т.е. способом, при котором каждое значение признака генеральной совокупности может несколько раз попасть в выборку. В случае бесповторного способа отбора, при котором каждое значение признака генеральной совокупности может попасть в выборку не более одного раза, приведенную формулу определения предельной ошибки выборки необходимо скорректировать на коэффициент, определяемый по формуле:

,

где - объем генеральной совокупности.

Окончательно формула для определения предельной ошибки выборки, сформированной бесповторным способом, имеет вид:

.

Получив основные результаты выборочного наблюдения (среднее значение выборки и предельную ошибку выборки), можно с заданной вероятностью определить границы, в которых будет находиться среднее значение генеральной совокупности:

,

где 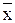- среднее значение генеральной совокупности;

- среднее значение выборки.

Приведенные формулы характерны для случая, когда признак совокупности принимает множество различных значений. Однако в генеральной совокупности, а, следовательно, и в выборке изучаемый признак может принимать всего два альтернативных значения. В этом случае вместо среднего значения генеральной совокупности говорят о доле признака в генеральной совокупности , а вместо среднего значения выборки − о частости .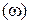

Долю признака в генеральной совокупности определяют по формуле:

,

где - количество интересующих значений признака в генеральной совокупности,

а частость признака в выборке по формуле:

,

где - количество интересующих значений признака в выборке.

Формула для определения предельной ошибки выборки, сформированной повторным способом отбора, имеет вид:

,

а для выборки, сформированной бесповторным способом отбора:

.

Определение с заданной вероятностью границ, в которых будет находиться доля признака в генеральной совокупности осуществляется по формуле:

.

Из четырех формул определения предельной ошибки выборки можно вывести формулы определения объема выборки, необходимого для получения результатов с заданной степенью точности. Они будут иметь вид:

- для выборки, сформированной повторным способом отбора:

(признак принимает множество различных значений);

(признак принимает два альтернативных значения);

- для выборки, сформированной бесповторным способом отбора:

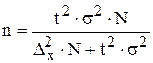(признак принимает множество различных значений);

(признак принимает два альтернативных значения).

Пример 9.1. Для изучения оснащения предприятия основными средствами было проведено 10 % выборочное обследование, в результате которого получены данные о распределении предприятий по среднегодовой стоимости основных средств.

Среднегодовая стоимость основных средств, млн.руб.	до 20	20 - 40	40 - 60	свыше 60
Количество предприятий

Определить:

1) с вероятностью 0,997 предельную ошибку выборочной средней и границы, в которых будет находиться среднегодовая стоимость основных средств всех предприятий генеральной совокупности;

2) с вероятностью 0,954 предельную ошибку выборки при нахождении доли и границы, в которых будет лежать удельный вес предприятий со стоимостью основных средств свыше 40 млн.руб.

Дата добавления: 2014-01-07