Тема 10. Корреляционно-регрессионный анализ

10.1. Виды связи и их особенности. Задачи корреляционно-регрессионного анализа

10.2. Парная регрессия. Оценка тесноты корреляционной связи

10.3. Множественная регрессия

10.1. Одной из основных задач статистики является выявление взаимосвязи между изучаемыми социально-экономическими явлениями.

Различают два основных вида связи: функциональную и стохастическую. При функциональной связи, каждому значению признака соответствует одно единственное значение признака 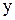. При стохастической связи, каждому значению признака соответствует множество значений признака 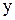. Частным случаем стохастической связи является корреляционная связь, при которой, каждому значению признака соответствует одно единственное среднее значение признака 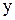. При этом называют факторным признаком, а 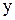− результативным признаком.

В теории статистики изучаются в основном стохастические и корреляционные зависимости между признаками. Корреляционный анализ предусматривает определение тесноты связи между двумя или более признаками с помощью специальных коэффициентов. Регрессионный анализ позволяет установить зависимость (форму связи) между рассматриваемыми признаками на основе построения регрессионной модели (уравнения регрессии).

В зависимости от количества факторных признаков, учитываемых в регрессионной модели, исследуется однофакторная (парная) или многофакторная (множественная) регрессия.

10.2. Количественной характеристикой корреляционной связи является линия регрессии. Линия регрессии представляет собой функцию, устанавливающую зависимость результативного признака 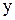от факторного признака . По форме линия регрессии бывает линейной и нелинейной (криволинейной), а по направлению связи − прямой и обратной. При прямой связи с увеличением значения признака увеличивается значение признака 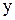и, наоборот. При обратной связи с увеличением значения признака значение признака 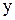уменьшается и, наоборот.

Как и любую функцию, линию регрессии можно представить аналитически, т.е. в виде уравнения. В статистике наиболее часто используется линейная форма представления линии регрессии. Линейное уравнение регрессии при парной корреляции имеет вид:

,

где - теоретическое значение результативного признака;

- значение факторного признака;

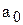, - коэффициенты уравнения регрессии, значения которых определяются по методу наименьших квадратов из системы двух уравнений следующего вида:

.

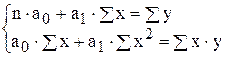Коэффициент регрессии определяет, на какую величину изменится значение результативного признака при изменении значения факторного признака на единицу.

Для определения, насколько процентов изменится результативный признак при изменении факторного на 1 %, рассчитывают коэффициент эластичности по формуле:

.

Построив уравнение регрессии, можно для каждого значения факторного признака определить соответствующее ему значение результативного признака .

Для моделирования на основе однофакторной модели (уравнения регрессии), необходимо проверить насколько точно она отражает линейную зависимость результативного признака от факторного признака , т.е. определить тесноту линейной связи между признаками.

Для определения тесноты связи между признаками необходимо рассчитать ряд показателей, одним из которых является коэффициент детерминации . Коэффициент детерминации рассчитывается по формуле:

,

где 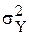- теоретическая дисперсия;

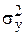- эмпирическая дисперсия, т.е. дисперсия признака полученного экспериментальным (опытным) путем.

Коэффициент детерминации принимает значения в интервале от 0 до 1. Чем ближе значение коэффициента детерминации к единице, тем более точно построенное уравнение регрессии описывает линейную корреляционную связь между признаками, и, наоборот, чем ближе значение коэффициента детерминации к нулю, тем менее точно уравнение регрессии описывает линейную корреляционную связь. Коэффициент детерминации, принимающий значение равное нулю, свидетельствует о полном отсутствии линейной корреляционной зависимости между признаками. Коэффициент детерминации, принимающий значение равное единице, соответствует ситуации, при которой наблюдается функциональная линейная зависимость между признаками.

Тесноту линейной связи между признаками можно проверить, рассчитав линейный коэффициент корреляции по формуле:

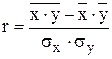или ,

где 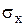, - среднее квадратическое отклонение соответственно признаков и .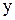

Линейный коэффициент корреляции принимает значение в интервале от -1 до +1 и, в отличие от коэффициента детерминации, характеризует не только тесноту линейной связи между признаками, но и ее направление. Если значение коэффициента положительное, то связь прямая, а если − отрицательное, то связь обратная. Линейный коэффициент корреляции равный нулю характеризует ситуацию, при которой полностью отсутствует линейная связь между признаками, а равный по модулю единице соответствует функциональной линейной связи признаков.

Пример 10.1. По данным о среднегодовой стоимости основных средств и объеме валовой продукции, построить уравнение регрессии и рассчитать показатели, характеризующие тесноту связи.

Среднегодовая стоимость основных средств, млн.руб.	Объем валовой продукции, млн.руб.

Дата добавления: 2014-01-07