Автокорреляция остатков

В экономических исследованиях достаточно часто возникают случаи, когда дисперсия остатков постоянна, но наблюдается их ковариация.Это явление называется автокорреляцией остатков.

При обработке временных рядов в силу адитивности векторов возмущений весьма реальным является предположение о том, что эти возмущения связаны между собой во времени, т.е. имеет место автокорреляция.Если существует корреляция между последовательными значениями некоторой независимой переменной, то будет наблюдаться также корреляция последовательных значений остатков.В этом случае нарушается гипотеза М (е, е^т ) = σ_u ² *E.

Но, при гетероскедастичности изменяется дисперсия остатков при отсутствии их корреляции, а при автокорреляции существует ковариация остатков при неизменной дисперсии.

. В простейшем случае имеет место авторерессионный процесс первого порядка.

ОПРЕДЕЛЕНИЕ: Возмущение U_t подчиняется авторегрессионому процессу первого порядка, если выполняются следующие условия:

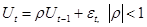
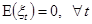[5.6]

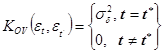
При автокорреляции остатков, как и при гетероскедастичности, диспер

сия остатков будет равна: М (е, е^т ) = σ_u ² *Ω.

Но матрица Ω имеет другой вид и ковариационная матрица в этом случае имеет вид:

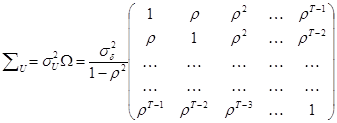
В этой матрице параметр р характеризует ковариацию каждого следую-

щего значения остатков с предыдущим.Например, если для остатков запи-

сать авторегрессионную модель первого порядка:

U_t = p u _{t – 1} + ε_t,

то р характеризует силу связи остатков в период t от их уровня в период t-1.

Если проигнорировать наличие автокорреляции и для оценивания пара-

метров модели применить 1-МНК, то возможны следующие последствия:

1. Оценки параметров модели могут быть несмещенними, но неэффективными,т.е. выборочные дисперсии вектора оценок могут быть неоправданно большими;

2. Статистические критерии t и F - статистики, полученные для классичесской линейной модели, не могут быть использованны, так как их использование не учитывает наличия ковариации остатков;

3. Неэффективность оценок параметров эконометрической модели как правило, приводят к неэффективным прогнозам, т.е. прогнозные зна

чения будут иметь большую выборочную дисперсию.

Для проверки наличия автокорреляции остатков рассмотрим два метода:

1. Критерий Дарбина-Уотсона;

2. критерий фон Неймана.

Дата добавления: 2014-01-07