Погрешность результата измерения

Оператор принимает решение (гипотезу Hi) в виде значения

y * = М * = y_i ’ = i с = 9211*10 ^–3 г (24)

Результат измерения представим как номер класса в виде

y (x) = y *[ x ]₀,

y * = i 10 ^{– m}, при х ’ _{i – 1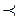} х ’ 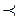х ’ _i. (25)

Запишем неравенства для эталонных интервалов

х ’ _{i – 1}[ x ]₀ < х ’ [ x ]₀ £ х ’ _i [ x ]₀, (26)

где х ’ – неизвестное значение, х ’ _i = i 10 ^{– m} – значение эталонной величины.

Введем термин погрешность результата измерения в следующем виде

e (x) = y (x) – x,

e (x) = y *[ x ]₀ - х ’ [ x ]₀ = (y * - х ’)[ x ]₀ = e ’ [ x ]₀, (27)

где e ’ = y * - х ’ – значение погрешности.

Выразим модуль | e ’| в виде двух зависимостей, отличающихся выбором интервала

| e ’| = | y * - x ’ _i | при x ’ = x ’ _I, (28)

| e ’| = | y * - x ’ _{i - 1}| при x ’ = x ’ _{i -1} (29)

Представим графики этих функций (24,25) и функции максимальных значений из | e ’| (24) и | e ’| (25), то есть функцию

max | e ’(y *)|

Рис. 5. Графики отклонений | e ’|

1 – | e ’| для зависимости (25), 2 – | e ’| для зависимости (24),

3 – max | e ’(y *)|

Запишем максимальную и оптимизированную погрешности

| e ’| _max = c = 10 ^{– m},

| e ’| _opt = min (max | e ’(y *)|) = 0.5* c = 0.5*10 ^{– m} . (30)

Принято выбирать в качестве оптимального значения результата измерения

y * _opt = x ’ _{i 1} +0.5* c ’ = x ’ _{i 1} + 0.5*10 ^{– m} =

.= x ’ _i - 0.5* c ’ = x ’ _i - 0.5*10 ^{– m}. (31)

В итоге модуль погрешности можно представить в виде

| e (x) | = | y * _opt - x ’| [ x ]₀ £ 0.5*10 ^{– m} [ x ]₀ = 0.5 c ’ [ x ]₀. (32)

Сравнение результатов измерения, полученных с помощью СИ разного класса

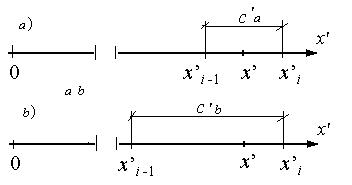
Рис. 6. Изображение результатов измерения

a) результат x ’ _i, полученный с помощью СИ(a), b) результат x ’ _i, полученный с помощью СИ(b).

Для сравнения результатов измерения, полученных с помощью СИ(a) и СИ(b), изобразим на рис. 6 числовые оси и значения x ’ _i, при этом для младших разрядов значений выполняется условие

c ’ _a < c ’ _b. (33)

В условиях, изображенных на рис. 6, результат, полученный с помощью СИ(a), можно рассматривать как предпочтительный по сравнению с результатом, полученным с помощью СИ(b), в виду неравенства (33).

Дата добавления: 2014-01-07